PHYSICS 432/750: COSMOLOGY
Winter 2003-2004

Instructor:
Prof. Michael S. Vogeley
Department of Physics
Office: 811 Disque Hall
Phone: 215-895-2710
Email: vogeley@drexel.edu
Office hours: TBA

Announcements
Course Meetings
Syllabus
Course Description and Philosophy
Course Outline
Textbook and Reading Assignments
Grading
Homework Assignments
Homework Hints
Homework Solutions
Exams
Course Schedule

Announcements

Welcome to the home page for Physics 432/750: Cosmology. Watch this space for important announcements and useful hints. Plan to use email to ask questions about homework assignments and the course readings so that I can give you timely feedback and send any relevant homework hints to everyone else in the class.

Course Meetings

Lecture times: Tuesday and Thurssday 9:30 - 10:50 a.m. in Disque 919.
If you will be unable to attend class, please notify me ahead of time or contact me as soon as possible.

Syllabus

This web page is the syllabus. If you're reading a printed copy, you may find the web page online at www.physics.drexel.edu/courses/Cosmology (note the capital "C" in Cosmology).

Course Description and Philosophy

Cosmology is the study of the universe as a whole and the formation and evolution of its contents. The relevant physics span from quantum mechanics to general relativity. Beginning from the solutions to Einstein's equations that yield the prediction of an expanding universe, we will work toward an astrophysical understanding of the origin of structure in the universe from both theoretical and observational perspectives.

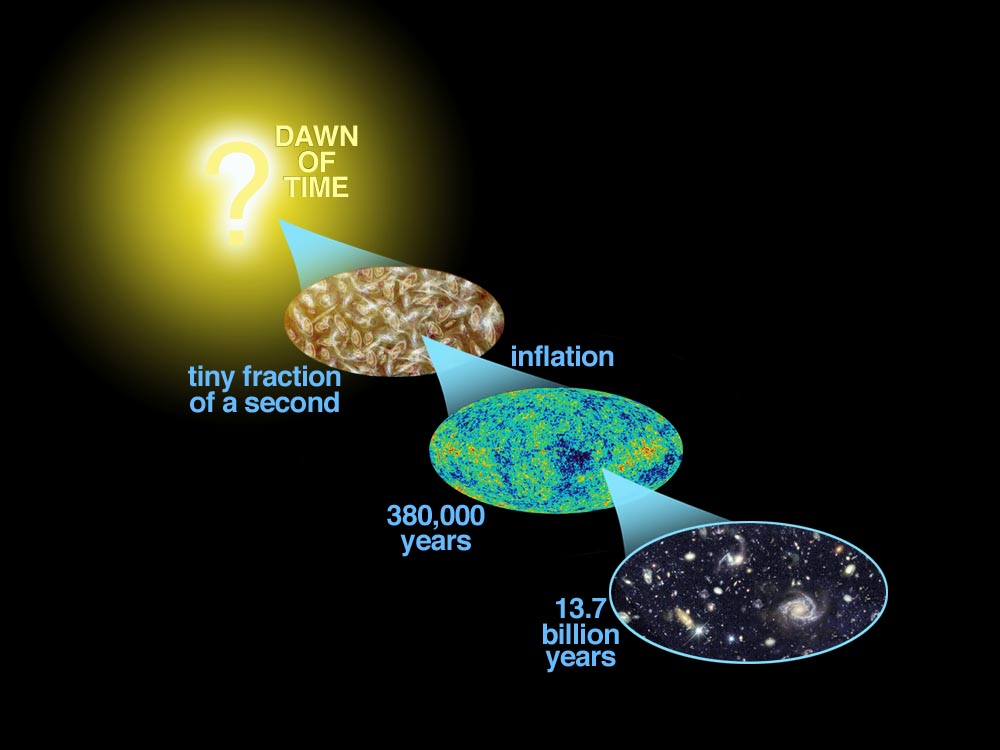
The field of cosmology is truly in a golden age, as we precisely map the distribution of galaxies at the present epoch, study the formation and evolution of stars, galaxies, and other bound objects, and probe fluctuations in matter and radiation when the universe was one thousandth of its current size. Together with theoretical advances that include the ability to simulate the evolution of cosmologically-interesting volumes of the universe, we are now able to make strong tests of proposed cosmological models. The questions of cosmology are central to physics: What is the matter and energy content of the universe? What drives the formation of structure? What were the initial conditions? Observations of the distribution of galaxies, the anistropy of the cosmic microwave background, and supernovae in distant galaxies indicate that a mere 5% of the mass-energy density in the universe is comprised of normal, baryonic matter. Roughly 25% is in the form of weakly-interacting dark matter. The remaining 70% - most of the universe - is in some form of dark energy similar to Einstein's cosmological constant.

The primary goal of this course is to expose advanced undergraduates and first and second year graduate students to the essential elements of astrophysical cosmology at a level that would allow them to read current literature in the field and to work through problems at the level required for beginning research.

Course Outline

Textbook and Reading Assignments

The required textbook is Cosmological Physics, by John A. Peacock, 1999, (Cambridge University Press: Cambridge), ISBN 0-521-42270-1 (paperback), 0-521-41072-X (hardcover). This book should be available in the Drexel bookstore. The text covers most of the material at a first-year graduate level.

Other useful texts include The Early Universe, by E. W. Kolb and M. S. Turner, 1990, (Addison-Wesley) and Principles of Physical Cosmology, by P.J.E. Peebles, 1993, (Princeton University Press). Also see chapter 12 of A First Course in General Relativity, by B. F. Schutz (Cambridge University Press).

Please read the assignments before class and prepare to ask questions.

See the Course Schedule below for the weekly reading assignments.

Grading

Grades will be based on the following weighting of different components of the course:
Homework: 30%
Midterm Exam: 30%
Final Exam: 40%

Note that this course includes two sections: Physics 432 for undergraduates and Physics 750-501 for graduate students. Grading for these sections will be as appropriate for the different levels of preparation.

Homework Assignments

Problem sets will be distributed in class. Use the PS or PDF files linked here in case you lose yours. There will be five homework sets, for which you will have roughly a week and a half to do each. Late homework will not be accepted. There will be no ``dropped homeworks.''

Solutions to the homework will be handed out in class on the due date (and posted on the web page), thus late homework will not be accepted. Please strive to present your answers in a neat, workmanlike fashion; the clarity of your solutions will count toward your grade.

Science is a collaborative enterprise and you are encouraged to discuss the homework problems. But you and you alone are responsible for the work that you turn in. Please write up your own solutions to the problems. Serious breaches of this policy will result in homework scores being divided by the number of ``participants.''

Homework 1. Due Thursday, January 22.
homework 1 problems (PDF)

Homework 2:
homework 2 problems (PDF)

Homework 3:
homework 3 problems (PDF)

Homework Hints

Watch this space and your email for helpful homework hints. Let me know if you'd like to add one!

Homework 2:
In problems 1 and 2 be careful that you use formulae for the coordinate distance that are accurate over the required range of redshift and cosmological parameters. An excellent approximate formula for flat universes may also be found in this paper from the Astrophysical Journal.
distance approx paper (PDF)
Q: In Problem 4, it's not clear to me how to relate the deltaM to the H0. Are we to calculate a delta flux proportional to deltaM, find the luminosity and then calculate a distance D(z)? If so, do we need red-shift information? Do all the standard candles have the same intrinsic luminosity?
A: First, recall that H_0 is the ratio of the recession velocity to the distance. The uncertainty in the intrinsic magnitude translates into an uncertainty in the distance to an object. Recall that m=-2.5log(f)+constant, where f\propto L/r^2, thus, the difference in apparent magnitude between objects depends on the ratio of their distances. It doesn't matter whether or not the four standard candles have the same intrinsic luminosity.
Q: In Problem 6, I have that vpeculiar = cz-H0r How does a r.m.s. value of vpeculiar come into this? Are we supposed to take a variation in vpeculair to get an error in H0? I'm somewhat confused as to exactly what you're looking for.
A: Right, at low redshift, the observed v = cz = H_0 r + v_pec. The point is to analyze what happens to the accuracy of H_0 estimates when v_pec is large/small compared to cz.
Q: On Problem 7, I interpret the 2D diagram to mean a plot with two y-axes: one with omega-matter and one with omega-vac and the age on the x-axis. Is this what you are looking for?
A: I mean a plot with Omega_vac on one axis and Omega_matter on the other, with the age shown by, e.g., lines with the same t (you could also do this with greyscale instensity). For a given t, there is a curve of values of Omega_vac and Omega_matter.
Large hints for problem 7 may be found in the text in chapter 9, p. 290.
Homework 3
Q: On Problem 1, did you mean to give a value for omega-radiation instead of omega-matter? If not, then omega-radiation is zero as is the radiation energy density.
A: The radiation energy density is very small today, but it's not zero. You can compute what it is today by using the measured temperature of the CMB.

Homework Solutions

Problem set solutions will appear here shortly after the homework is due. Homework 1 solutions:
homework 1 solutions (PDF)

Homework 2 solutions
homework 2 solutions (PDF)

Homework 3 solutions
homework 3 solutions (PDF)

Exams

The midterm will be an in-class exam (1h 20m long) given during week 6. The final will be given during finals week, at 9:00 a.m., Thursday, March 18. The problems on each will be approximately half open book, half closed book. The final exam will include material from the entire course, but with more weight given to the second half of the course.

Course Schedule

This schedule is subject to change. Watch for announcements.

Week Class Dates Topics Reading Homework Exams
1 January 6, 8 Isotropic Universe ch. 3 HW1
2 January 13, 15 Age and Distance Scales ch. 5  
3 January 20, 22 Hot Big Bang ch. 9 HW2
4 January 27, 29 Inflationary Cosmology ch. 11
5 February 3, 5 Matter in the Universe ch. 12 HW3
6 February 10, 12 Galaxies and their Evolution ch. 13 Midterm
7 February 17, 19 Dynamics of Structure Formation ch. 15 HW4
8 February 24, 26 Cosmological Density Fields ch. 16
9 March 2, 4 Galaxy Formation ch. 17 HW5
10 March 9, 13 Cosmic Background Fluctuations ch. 18
11 No Class Final Exam

Last update: January 9, 2004