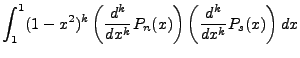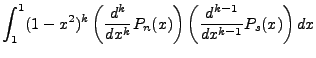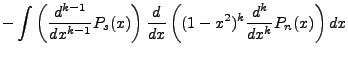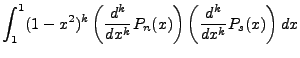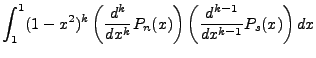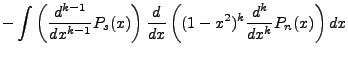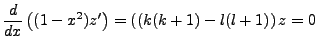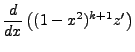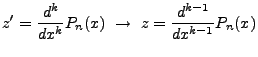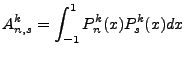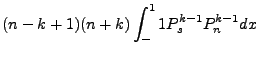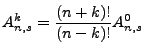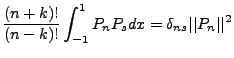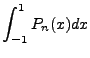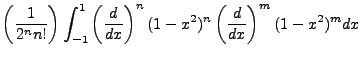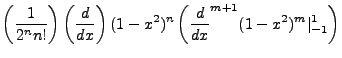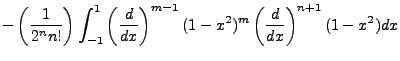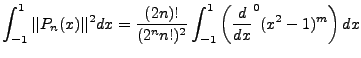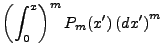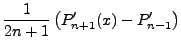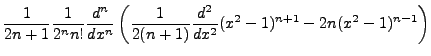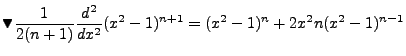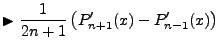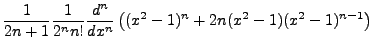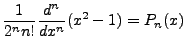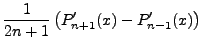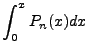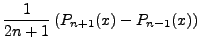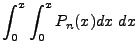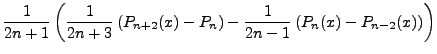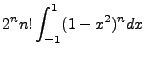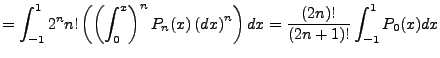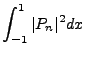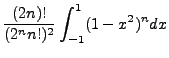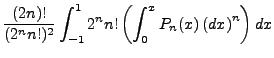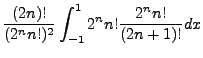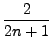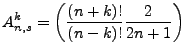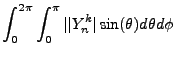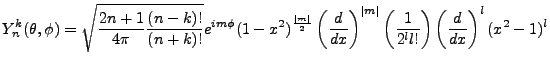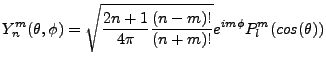Next: Radial side
Up: The Angular Component
Previous: A closer look
Define
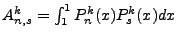 , then by separation of variables:
, then by separation of variables:
Introduce
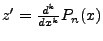 . From our previous discussion, we find that,
. From our previous discussion, we find that,
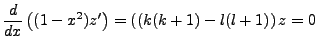 |
(3.15) |
Or just as easily,
Here we need to compensate for the following: The z used in this previous equation was built with:
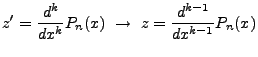 |
(3.16) |
Thus we must shift
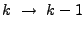 . Thus,
. Thus,
We can find 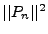 as another separation of variables chain:
as another separation of variables chain:
The non-integral part equals zero, the integral component cycles up on the n derivative and down
on the m derivative. Of course, 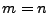 , but we maintain the separation for the sake of derivation.
The final result of the cycle gives:
, but we maintain the separation for the sake of derivation.
The final result of the cycle gives:
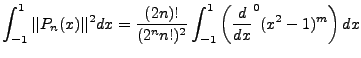 |
(3.18) |
To solve the latter integral, we introduce two identities:
So we follow through,
We follow through this derivation cycle n times, splitting each P value as per the above identity.
The 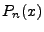 integral becomes the
integral becomes the 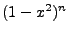 as identified above and he array
as identified above and he array 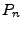 will be spread from
values of
will be spread from
values of
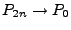 . If we integrate both sides of the equation over the Legendre function
range, [-1,1], all said values of
. If we integrate both sides of the equation over the Legendre function
range, [-1,1], all said values of 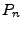 will vanish except
will vanish except 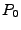 . The prefactors from the expansion give:
. The prefactors from the expansion give:
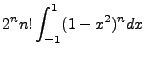 |
|
|
|
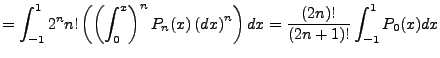 |
|
|
(3.20) |
But properly,
From this we conclude,
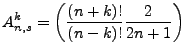 |
(3.22) |
Of course, we cannot neglect the symmetric components of theta, which give us an additional normalization of 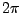 ,
thus the final normalization condition,
,
thus the final normalization condition,
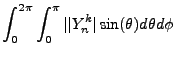 |
(3.23) |
Re-tagging our variables appropriately, the normalized Associated Legendre Polynomial is,
Or in simplified notation,
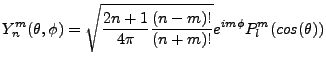 |
(3.24) |
.



Next: Radial side
Up: The Angular Component
Previous: A closer look
tim jones
2009-02-11