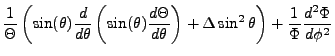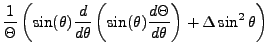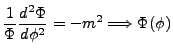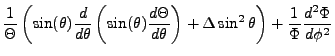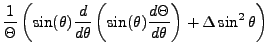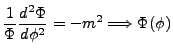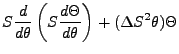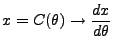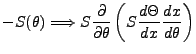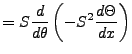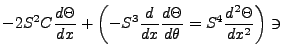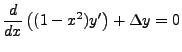Next: A closer look
Up: The Legendre and Laguerre
Previous: The Hydrogen Calculation using
Once again, it is reasonable to assume a certain dimensional independence which enables separation of variables in
terms of the 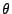 and
and 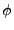 components. Under this regime:
components. Under this regime:
The 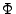 side of the equation was quickly solved.
We can recast this equation in the following variations, where we let C represent
side of the equation was quickly solved.
We can recast this equation in the following variations, where we let C represent
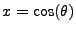 and S
and S
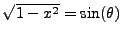 ; we introduce the notation
; we introduce the notation
 which represents an introduction of a new idea into the
stream of derivation, and
which represents an introduction of a new idea into the
stream of derivation, and
 is followed by the immediate consequence of this new idea; we then consider the
is followed by the immediate consequence of this new idea; we then consider the 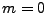 case.
case.
As we further press on this equation, we shall find it suggesting its own solution,
even betraying the separation constant 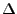 .
.
Subsections



Next: A closer look
Up: The Legendre and Laguerre
Previous: The Hydrogen Calculation using
tim jones
2009-02-11