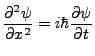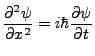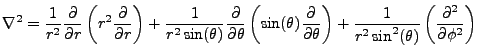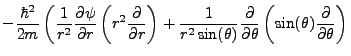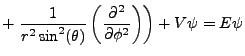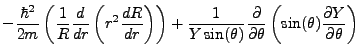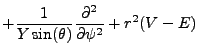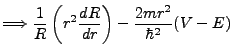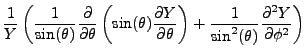The Hydrogen Calculation using Schrödinger's equation

Enter Schrödinger. He proposed that an object in quantum mechanics obeys the wave equation,

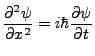$$\frac{\partial^2 \psi}{\partial x^2}=i\hbar\frac{\partial \psi}{\partial t}$$ (2.1)

But of course, the Hydrogen atom does not live in one dimension. We must move to three dimensions, using spherical coordinates as the most natural setting for our derivation.

In spherical coordinates the Laplacian becomes:

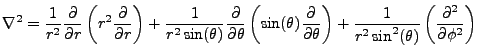$$\nabla^2=\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2 \frac{... ...ht)+\frac{1}{r^2 \sin^2(\theta)}\left(\frac{\partial^2}{\partial \phi^2}\right)$$ (2.2)

Schrödinger's equation becomes:

$$-\frac{\hbar^2}{2m}\left(\frac{1}{r^2}\frac{\partial \psi}{\parti... ...partial \theta}\left(\sin(\theta)\frac{\partial}{\partial \theta}\right)\right.$$

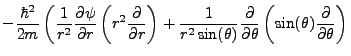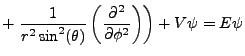$$+ \left.\frac{1}{r^2 \sin^2(\theta)}\left(\frac{\partial^2}{\partial \phi^2}\right)\right) + V\psi = E\psi$$ (2.3)

If we assume that the solutions can be found through separation of variables:

$$\psi(r,\theta, \phi) = R(r)Y(\theta,\phi) \rightarrow$$

$$-\frac{\hbar^2}{2m}\left(\frac{1}{R}\frac{d}{dr}\left(r^2\frac {d... ...al}{\partial \theta}\left(\sin(\theta)\frac{\partial Y}{\partial \theta}\right)$$

$$+\frac{1}{Y \sin(\theta)}\frac{\partial^2}{\partial \psi^2} + r^2(V-E) =$$ 0

$$\Longrightarrow \frac{1}{R}\left(r^2\frac{dR}{dr}\right)-\frac{2mr^2}{\hbar^2}(V-E) = \Delta ,$$

$$\frac{1}{Y}\left(\frac{1}{\sin(\theta)}\frac{\partial}{\partial \... ...}\right) + \frac{1}{\sin^2(\theta)} \frac{\partial^2 Y}{\partial \phi^2}\right) = -\Delta$$ (2.4)

We have divided, and now we are ready to solve. The radial term contains the potential V, which is a function of r for hydrogen. It is the more complex of the two, and so we seek to explore the angular term first. Our analysis will find the 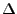$\Delta$ constant of separation in its exact form, enabling a strong attempt at solving the radial equation.