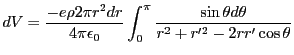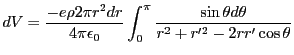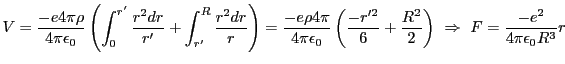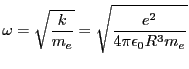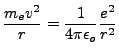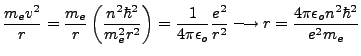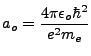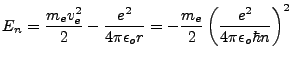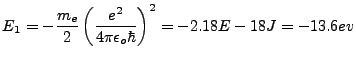Next: The Hydrogen Calculation using
Up: The Legendre and Laguerre
Previous: The Legendre and Laguerre
We first consider an early model of the hydrogen atom, (Thompson 1903) [1]. In this model, the atom is a blob of uniformly distributed positive charge, a sphere of radius 1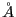 and charge
and charge 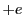 . The electron is considered to exist as a point like particle within this sphere. Breaking the sphere up into
infinitesimal shells, each shell will contribute a potential to the electron of
. The electron is considered to exist as a point like particle within this sphere. Breaking the sphere up into
infinitesimal shells, each shell will contribute a potential to the electron of
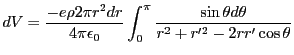 |
(1.1) |
Where
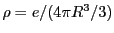 , r is the radius of the shell, and r' is the location of the electron relative to the center of the sphere. Considering shells of radius less than the position of the electron, and those greater, the potential is
, r is the radius of the shell, and r' is the location of the electron relative to the center of the sphere. Considering shells of radius less than the position of the electron, and those greater, the potential is
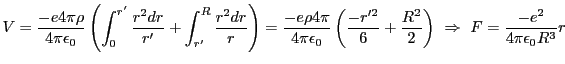 |
(1.2) |
Similar in form to the harmonic potential, 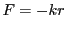 , we have,
, we have,
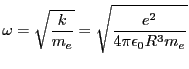 |
(1.3) |
We divide by 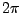 and use known constants to find that we expect a frequency
of
and use known constants to find that we expect a frequency
of
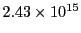 Hz corresponding to 123 nm wavelength. This is
approximately the Lyman-alpha wavelength (121.5 nm), but does not account for
the infinite spectrum that Hydrogen actually exhibits. Nor does this model
incorporate Planck's discovery of quantization of radiation.
Hz corresponding to 123 nm wavelength. This is
approximately the Lyman-alpha wavelength (121.5 nm), but does not account for
the infinite spectrum that Hydrogen actually exhibits. Nor does this model
incorporate Planck's discovery of quantization of radiation.
The earliest model of the hydrogen atom that accounted for
Planck's discovery that a proper explanation of the blackbody radiation spectrum
could only be achieved through quantization of the
energy released by atoms was achieved by Niels Bohr.
The model had the following properties, as summarized by Bohr [2,3]:
- The electron emits radiation when transitioning from one discreet
state to the next.
- Classical mechanics is valid when the electron is not transitioning.
- In transition from a state to another, energy differences being
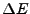 , a photon of frequency
, a photon of frequency
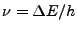 is emitted.
is emitted.
- Angular momentum is quantized and identifies permitted orbits. It is
always a natural number multiple of
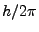 .
.
The model is amazingly simple, but manages to correctly predict the ground
state energy level. It goes as follows. Since we assume the laws of classical
mechanics hold in non-transition periods, the electron obeys the Coulomb force law
and the centripetal acceleration formulation:
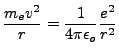 |
(1.4) |
Under the quantization of orbital angular momentum, we can write
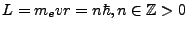 . This number, n,
will be seen throughout this derivation as a key and important variable, the angular momentum quantum number. From our
definition of L, we find that,
. This number, n,
will be seen throughout this derivation as a key and important variable, the angular momentum quantum number. From our
definition of L, we find that,
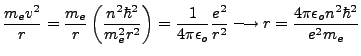 |
(1.5) |
The smallest possible orbit is when 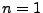 . This is called the Bohr radius, and is given as
. This is called the Bohr radius, and is given as
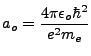 |
(1.6) |
Energy is the sum of its Kinetic and Potential partitions, and given our previous results,
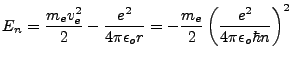 |
(1.7) |
It was a great result that this formula predicts the ground state energy and excited energy states of the electron:
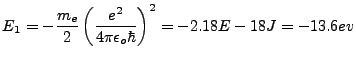 |
(1.8) |
The model also gives a more accurate picture of the spectrum of hydrogen, where
we can use
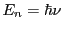 to find the corresponding frequencies.
But this is not good enough. This model tells us nothing about why and how the transitions are made. It is rather ad hoc.
to find the corresponding frequencies.
But this is not good enough. This model tells us nothing about why and how the transitions are made. It is rather ad hoc.
Bohr also introduced a helpful principle in Quantum Mechanics, the Correspondence Principle, the idea that Quantum Mechanical
calculations must limit to classical results when the census of quantum numbers tends towards infinity.



Next: The Hydrogen Calculation using
Up: The Legendre and Laguerre
Previous: The Legendre and Laguerre
tim jones
2009-02-11