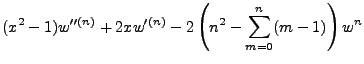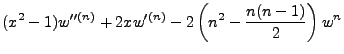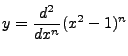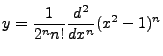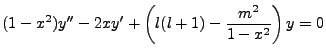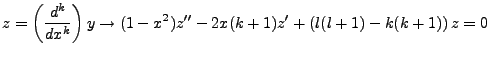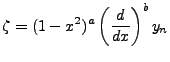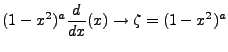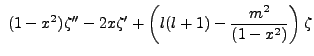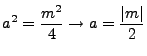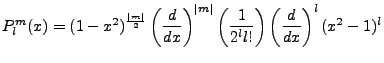Next: Normalization for final result
Up: The Angular Component
Previous: The Angular Component
Let us take a careful look at the equation,
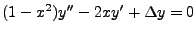 |
(3.2) |
We note that the x derivative of 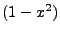 is
is 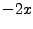 . This is highly suggestive that the kernel of
our function is
. This is highly suggestive that the kernel of
our function is 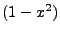 itself. The multiple derivatives suggest something a la
itself. The multiple derivatives suggest something a la
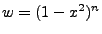 . So
let us explore this kernel. Its first derivative is
. So
let us explore this kernel. Its first derivative is
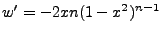 or
or
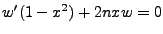 Define
Define 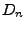 to be the nth derivative of this latter equation. Then we have the
following formulation:
to be the nth derivative of this latter equation. Then we have the
following formulation:
If we have instead
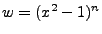 :
:
This latter equation is in the same form as our original equation. That is,
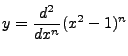 |
(3.3) |
Or, if we so choose,
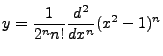 |
(3.4) |
This is the so called Legendre Polynomial, denoted by 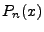 We so assign
We so assign
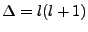 . But what of the
. But what of the 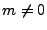 cases? In such a
situation, our equation of interest can be cast as:
cases? In such a
situation, our equation of interest can be cast as:
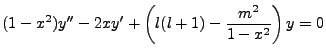 |
(3.5) |
Let us continue the derivation series from above; Recall that
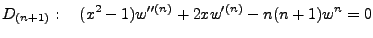 |
(3.6) |
Continuing the process we get,
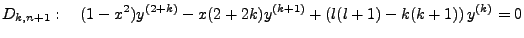 |
(3.7) |
Or, in the spirit of what we have done thus far, write:
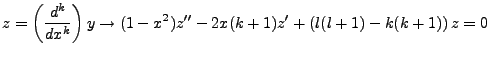 |
(3.8) |
This does not yield the correct formulation. When we recast the original equation as:
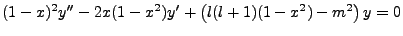 |
(3.9) |
This easily suggests the following form for our final function:
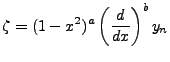 |
(3.10) |
To find what form a and b take, we consider 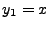 with
with 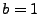 since clearly b must be be
a positive integer:
since clearly b must be be
a positive integer:
Upon the expansion of the latter equation for x, we can match each term with its coefficients.
These coefficients must equal zero to satisfy the equation. It is easiest to take the highest
coefficients of x:
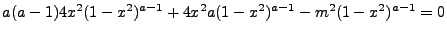 |
|
|
|
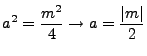 |
|
|
(3.12) |
Here m=1, but we assume the ansazts of generalization whereby, sans a normalization constant,
the full solution of our angular equation is the associated Legendre Function,
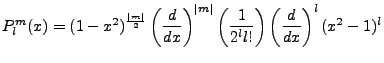 |
(3.13) |



Next: Normalization for final result
Up: The Angular Component
Previous: The Angular Component
tim jones
2009-02-11