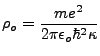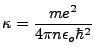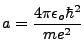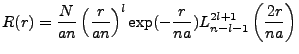Next: Normalization of the Radial
Up: The Legendre and Laguerre
Previous: Normalization for final result
Granted that
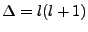 , the radial equation becomes simply:
, the radial equation becomes simply:
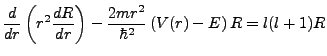 |
(4.1) |
When finding solutions to such equations, it is generally in our best interest to
isolate the leading derivatives. We can do so with the substitution:
Here we have considered the bound states of the electron (of course) where 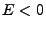 .
.
Typically, one looks and supposes asymptotic solutions. For
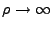 ,
,
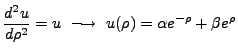 |
(4.3) |
But of course, finiteness requires that 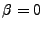 As
As
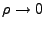 , the
, the 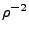 term dominates
term dominates 
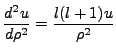 |
(4.4) |
The solution to this equation is interesting to derive. We suppose the existence
of some function 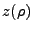 , and rewrite the equation thereby:
, and rewrite the equation thereby:
The trick here is to assume that there exist a 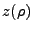 such that the previous equation
is a differential equation with constant coefficients, i.e.:
such that the previous equation
is a differential equation with constant coefficients, i.e.:
Our characteristic equation follows from:
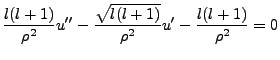 |
(4.7) |
It is easy to show the resulting characteristic is
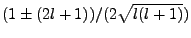 with
solutions:
with
solutions:
Since this solution contains the zero point, 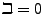 , and we can write our asymptotic general solution
in total as
, and we can write our asymptotic general solution
in total as
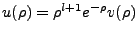 , where
, where 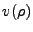 is some unknown function which
properly completes the radial function and is to be found. Reformulating the equation thus far,
is some unknown function which
properly completes the radial function and is to be found. Reformulating the equation thus far,
With the radial equation as,
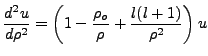 |
(4.9) |
We can plug in the values we found above to reformulate the equation in terms of v. Via algebra
which can be easily done in mind, we find:
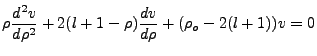 |
(4.10) |
Following typical derivations (though we will part with it eventually), we assume a
solution of a series solution form,
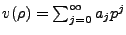 . Done so, the prior
equation becomes,
. Done so, the prior
equation becomes,
Obviously the series must terminate dynamically, i.e.
Our new recursion equation is:
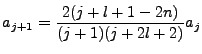 |
(4.12) |
We consider a few sample results of 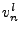 . E.g.
. E.g.
We can go on ad infinitum, but we seek an analytical solution to this equation.
The asymptotically suggested form gives us a starting point for its completing function. We also suspect that the
solution might follow the onion-derivative similar to that of the angular solution. With these educated guesses, we
start as follows: We assume the solution has a kernel
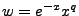
We had plugged in 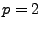 as a simple test of low level results. Take the derivative of the
latter equation and find,
as a simple test of low level results. Take the derivative of the
latter equation and find, 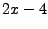 a la
a la
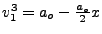 . One could follow through
this examination ad infinitum, but we already know the ending to this story so we assume immediately
that we have happened upon the correct solution form, i.e.
. One could follow through
this examination ad infinitum, but we already know the ending to this story so we assume immediately
that we have happened upon the correct solution form, i.e.
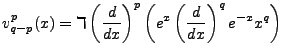 |
(4.14) |
When
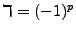 , the above equation is the associated Laguerre Polynomial,
, the above equation is the associated Laguerre Polynomial, 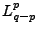 . We can bring this all
home as follows. We consider our
. We can bring this all
home as follows. We consider our 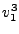 example. In that case, for
example. In that case, for 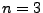 ,
, 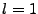 , we can write the the
v completing function with coefficients in terms of the recursion variables. Using
, we can write the the
v completing function with coefficients in terms of the recursion variables. Using
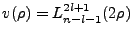 , which,
due to the multiplication by two matches our
, which,
due to the multiplication by two matches our 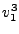 example,
example,
Now
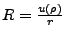 , where:
, where:
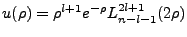 |
(4.15) |
But with 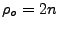 , and
, and
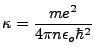 |
(4.16) |
Let
which is the Bohr Radius we had previously derived. Then
we write
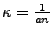 . Thus
. Thus
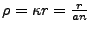 . Ergo
. Ergo
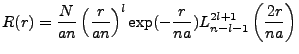 |
(4.17) |
The normalization factor N is determined as follows.
Subsections



Next: Normalization of the Radial
Up: The Legendre and Laguerre
Previous: Normalization for final result
tim jones
2009-02-11
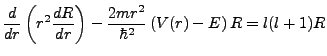
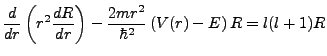
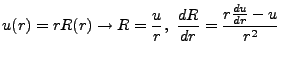
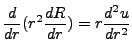
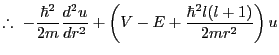
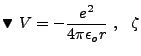
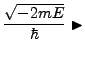
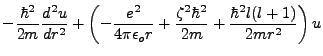
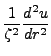
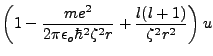
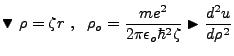
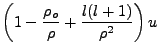
![]() ,
,
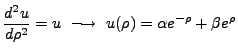
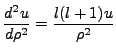
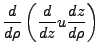
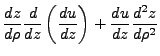
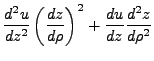
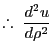
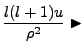

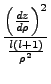
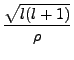
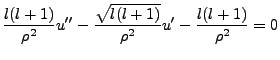
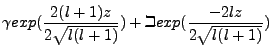
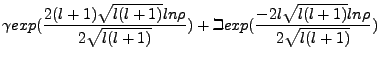
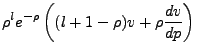
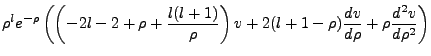
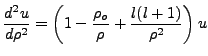
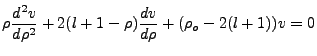
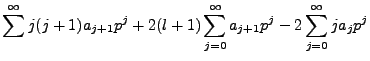
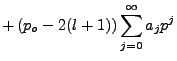
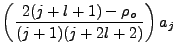
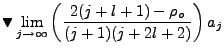
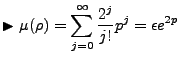
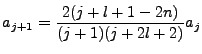
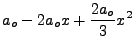
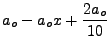
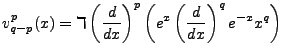
![]() , where:
, where: