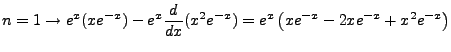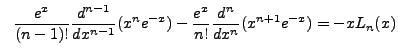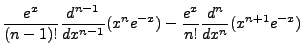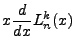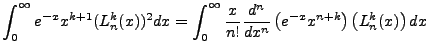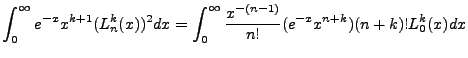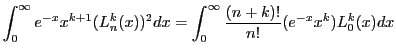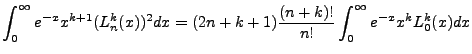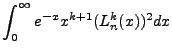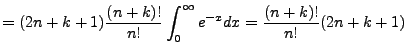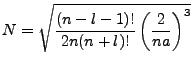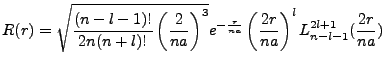Next: Final Form
Up: Radial side
Previous: Radial side
Key to normalizing the radial term is the normalization of the Laguerre
Polynomials. This task will not be as facile as was normalization for
the Legendre Polynomials.
Given that
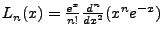 , we note the
following:
, we note the
following:
In the same way, we find that:
One final note is to demonstrate the following for one case and assume the rest of the cases by
assumed induction:
Putting the above three results into place, we find that:
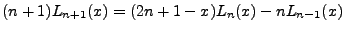 |
(4.20) |
We can derive another important and useful identity as follows:
But we are using associated Laguerre Polynomials, so we need to extend these identities. We
will not work out the details, but taking the derivatives of the previous identities gives
us the associated identities:
The solution we found for the radial equation took the form
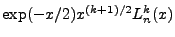 .
The normalization equation for this formulation gives:
.
The normalization equation for this formulation gives:
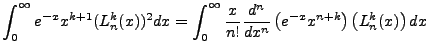 |
|
|
(4.23) |
Applying integration by parts n times, cycling up on the left derivative and down on the right Laguerre, using
the derivative formula above, we land at:
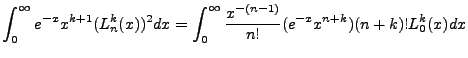 |
(4.24) |
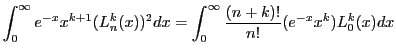 |
(4.25) |
From the identity, we have:
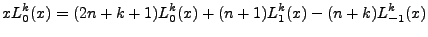 |
(4.26) |
When we plug this into the integral to wash away the x, all terms integrate to zero except 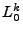 , and our integral becomes:
, and our integral becomes:
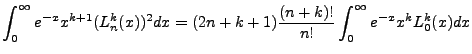 |
(4.27) |
With
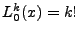 , and a integration by parts performed on the remaining integral (cycling down the
, and a integration by parts performed on the remaining integral (cycling down the 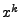 so that
the
so that
the 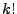 values cancel, we get:
values cancel, we get:
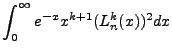 |
|
|
|
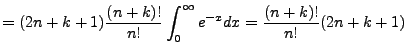 |
|
|
(4.28) |
Now when we adjust this representation for our own, i.e.
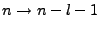 and
and
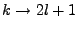 , the
normalization constant becomes
, the
normalization constant becomes
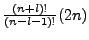 . Incorporating the fact that we must convert
. Incorporating the fact that we must convert
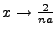 , this calls upon an additional normalization factor of
, this calls upon an additional normalization factor of
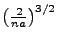
Thus the radial normalization is:
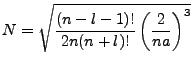 |
(4.29) |
Our final radial equation becomes:
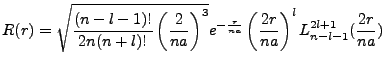 |
(4.30) |



Next: Final Form
Up: Radial side
Previous: Radial side
tim jones
2009-02-11
![]() , we note the
following:
, we note the
following:
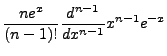
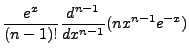
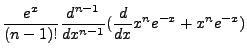
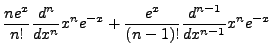
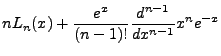
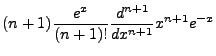
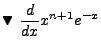
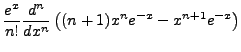
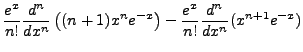
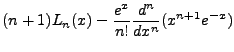
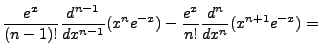 ?
?