


Next: A relaxed derivation of
Up: A More Fundamental Analysis
Previous: A More Fundamental Analysis
The conditions for the convergence of the simultaneous over-relaxation method
are found via Kahan's Theorem (Equaton 3.10). Note that
Since
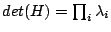 , (
, (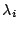 are eigenvalues of H), and the spectral radius is defined by
are eigenvalues of H), and the spectral radius is defined by
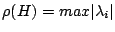 ,
,
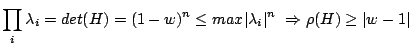 |
(3.10) |
Now the Fundamental Theorem of Linear Iterative Methods (see final section) tells us we
have convergence if 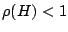 , and since
, and since
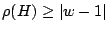 ,
Obviously
,
Obviously 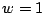 is Jacobi-GS, and
is Jacobi-GS, and 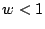 is foolish, so we consider
is foolish, so we consider 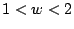 . It is now
our task to find which value in this region is most efficient.
. It is now
our task to find which value in this region is most efficient.



Next: A relaxed derivation of
Up: A More Fundamental Analysis
Previous: A More Fundamental Analysis
Timothy Jones
2006-02-24