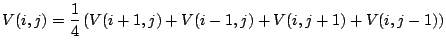Jacobi, Gauss-Seidel Method

The Jacobi method proposes to impose a grid over our physical environment. This grid is the standard square grid type, whereby the mean value method can only sample four points:

This gives

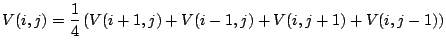$$V(i,j)=\frac{1}{4}\left(V(i+1,j)+V(i-1,j)+V(i,j+1)+V(i,j-1)\right)$$ (2.1)

If we now imagine taking this average over a i by j grid under the boundary constraints in an iterative process, we might see that after many iterations the boundary conditions will have 'flowed' by averaging throughout the system, a process called 'relaxing'. Once the iteration process gives negligible change in our grid, we have found a numerical solution to our potential problem. Under the right conditions, convergence is guaranteed (more on this later).

Whereas the Jacobi method sums the potential as the average of its neighbors in their pre-determined state (i.e. from the previous set of iterations), the Gauss-Seidel (GS) method proposes the use of the latest numbers as they become available.

In Simultaneous Over Relaxation (SOR) we push these methods even further, for if we define $\Delta V = V_{New}(i,j)-V_{Old}(i,j)$, then SOR proposes to force that change by some factor $\alpha > 1$:

$$V_{New}(i,j)=V_{Old}(i,j)+ \alpha \Delta V$$

. Finding the right $\alpha$ value without wrecking the process is the point of this report.