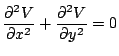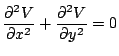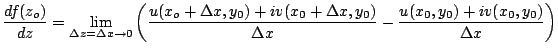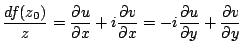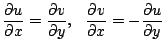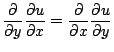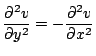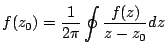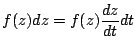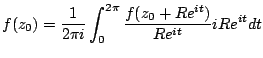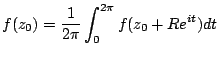Next: Jacobi, Gauss-Seidel Method
Up: Simultaneous (successive) Over Relaxation
Previous: Simultaneous (successive) Over Relaxation
In an electrical vacuum, the electrical potential
obeys Laplace's equation:
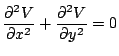 |
(1.1) |
A real-valued function is considered harmonic in a domain D if all of
its second-order partial derivatives are continuous in D, and if at
each point in D the function satisfies Laplace's equation [1].
Such functions come from the real and imaginary parts of complex analytical
functions.
Consider the function:
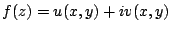 |
(1.2) |
We assume the derivative of this function exists at
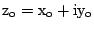 . We let
. We let
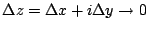 along the x and y axis
independently, which is to say,
along the x and y axis
independently, which is to say,
Likewise for
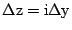 , such that we have the set of
equations,
, such that we have the set of
equations,
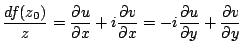 |
(1.3) |
These are better known as the Cauchy-Riemann equations,
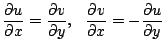 |
(1.4) |
The demand that
gives
Which is simply Laplace's equation, establishing our claim that
potential functions are components of complex functions. With this fact
comes the many useful tools of complex analysis.
Specifically, Cauchy's Integral Formula reads,
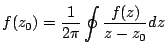 |
(1.5) |
for some contour. If we parameterize that contour with
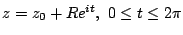 , and
This gives
This is better known as the Mean-Value property,
, and
This gives
This is better known as the Mean-Value property,
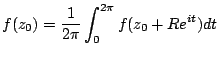 |
(1.6) |
A harmonic function evaluated at some point is equal to the average value
of that function around some circle (or sphere) centered at that point. The Jacobi method follows directly from this.



Next: Jacobi, Gauss-Seidel Method
Up: Simultaneous (successive) Over Relaxation
Previous: Simultaneous (successive) Over Relaxation
Timothy Jones
2006-02-24