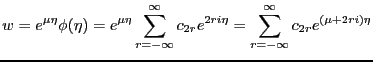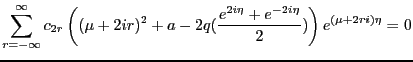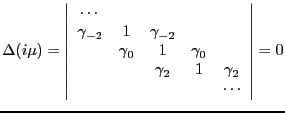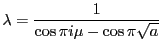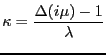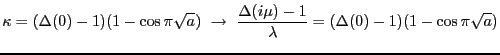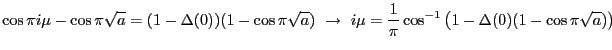Next: Sträng's recursion formula for
Up: Mathieu's Equation, solution, and
Previous: Basics and Flouqent's Theorem
With Floquent's theorem we assume a series solution, due to G. W. Hill,
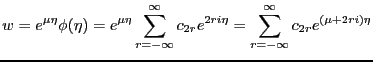 |
(2.5) |
When we put this into Mathieu's equation,
matching terms in power of r, we get the equation
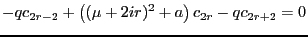 |
(2.6) |
Multiplying through by 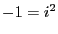 , and then dividing by the middle term,
, and then dividing by the middle term,
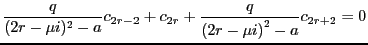 |
(2.7) |
We now define
That these coefficents, 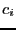 have non-trivial solutions
requires the infinite determinant
have non-trivial solutions
requires the infinite determinant  to vanish for noninfinite r:
to vanish for noninfinite r:
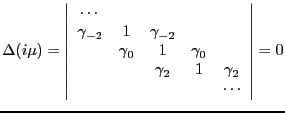 |
(2.8) |
But of course, this is not a simple object to understand and solve. We can
approach this problem from a rather clever angle introduced by E. T. Whittaker.
Consider the function
Like our determinant, 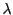 has a simple pole at
has a simple pole at
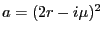 ,
so that the function
,
so that the function
has no singularities if 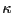 is
chosen properly and is bound at infinity, where
is
chosen properly and is bound at infinity, where
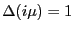 since
the
since
the 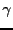 functions all vanish and the diagonal term is all that remains,
and
functions all vanish and the diagonal term is all that remains,
and
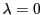 since
since 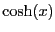 limits to zero as x tends towards
infinity.
limits to zero as x tends towards
infinity.
By Liouville's theorem (of complex calculus), since this
limits to a constant, it is a constant always, so we have
Next we consider the 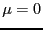 case and find,
case and find,
Next we suppose that 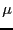 is chosen to satisfy our requirement that the determinant vanish.
We thus have
is chosen to satisfy our requirement that the determinant vanish.
We thus have
Recall that our solution took the form,
This solution will be unbounded unless
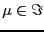 , in which case we have
, in which case we have
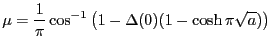 |
(2.9) |
We can easily encode this result, say,
if(a>=0){ mu=acos( 1 - (d[100])*(1-cos(pi*sqrt(a)))) / (pi);}
if(a<0){ mu=acos( 1 - (d[100])*(1-cosh(pi*sqrt(fabs(a))))) / (pi);}
if (mu != mu){mu=0.000000;} //If mu=nan then make it zero
But first we must calculate 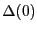 . This task has been made
exceedingly simple by the recent work of J. E. Sträng [5]
who has found an efficient recursion formula.
. This task has been made
exceedingly simple by the recent work of J. E. Sträng [5]
who has found an efficient recursion formula.



Next: Sträng's recursion formula for
Up: Mathieu's Equation, solution, and
Previous: Basics and Flouqent's Theorem
tim jones
2008-07-07