


Next: The partition
Up: Detailed Derivation of the
Previous: The Integration
To extract 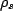 we now need to trace over the environmental variables, i.e. average out the environmental degrees of freedom. We can most quickly see that,
we now need to trace over the environmental variables, i.e. average out the environmental degrees of freedom. We can most quickly see that,
![$\displaystyle Tr_e[H_i(t),\rho_{se}]=0$](img62.png) |
(4.1) |
as 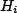 is linear with
is linear with 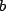 and
and
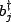 ,
,
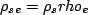 ,
and it is self evident that
Thus we are left with,
,
and it is self evident that
Thus we are left with,
![$\displaystyle \frac{d\rho_s(t)}{dt}=-\frac{1}{\hbar^2}\int^t_0 Tr_e\left[H_i(t),[H_i(t'),\rho_{se}(t')]\right]dt'$](img67.png) |
(4.2) |
To proceed from here will require some care.
Subsections
Timothy Jones
2006-10-11