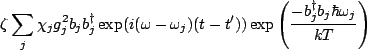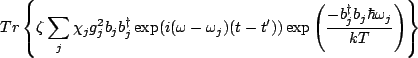Next: Case B
Up: The Trace
Previous: The partition
The first term we can extract is,
We recall that
so we can rewrite the term as (with
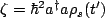 and
and
![$ \chi_i = \left[1-\exp\left(\frac{-\hbar \omega_i}{kT}\right)\right]$](img76.png) ),
It is easily seen that when we take the trace, all terms will involve
),
It is easily seen that when we take the trace, all terms will involve
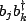 and will vanish unless
and will vanish unless 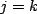 , so we can write
the term as,
But again, we can use the same argument to write the term as,
We can now easily take the trace, noting that
, so we can write
the term as,
But again, we can use the same argument to write the term as,
We can now easily take the trace, noting that
![$ Tr[B\rho] = <B>$](img82.png) , and with
, and with
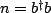 with
with
![$ [b,b^{\dagger}]=1$](img84.png) .
For the reader interested in the total details of the previous calculation, [1] is a good reference, where it is also demonstrated that, for example,
.
For the reader interested in the total details of the previous calculation, [1] is a good reference, where it is also demonstrated that, for example,
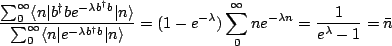 |
(4.3) |
In any case, we now have a general formula we can use, that is,
The other non zero trace will be, with
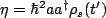 and
and
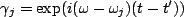



Next: Case B
Up: The Trace
Previous: The partition
Timothy Jones
2006-10-11
![$\displaystyle \zeta\left[\sum_jg_jb_j\exp(i(\omega-\omega_j)t)\right] \left[\su...
...ight] \prod_i \chi_i\exp\left(\frac{-b_i^{\dagger}b_i\hbar \omega_i}{kT}\right)$](img77.png)
![$\displaystyle \zeta\left[\sum_jg_j^2b_jb_j^{\dagger}\exp(i(\omega-\omega_j)(t-t...
...right]\prod_i \chi_i\exp\left(\frac{-b_i^{\dagger}b_i\hbar \omega_i}{kT}\right)$](img80.png)