The Integration

Beginning with Equation 2.10, we take the first integration to get,

$$\rho_{se}(t)=\rho_{se}(0)+\frac{1}{i\hbar}\int^t_0\left[H_i(t'),\rho_{se}(t')\right]dt'$$ (3.1)

Taking this result, we plug it into itself and get,

$$\rho_{se}(t)=\rho_{se}(0)+\frac{1}{i\hbar}\int^t_0\left[H_i(t'),\... ...bar^2}\int^t_0\int^{t'}_0\left[H_i(t'),[H_i(t''),\rho_{se}(t'')\right]dt''dt'\$$ (3.2)

Quoting Narducci, ``now we do something unexpected'' and differentiate this equation. Since,

$$\frac{d\rho_{se}}{dt}\vert _{t=0}=\frac{1}{i\hbar}[H_i(0),\rho_{se}(0)]$$

and

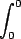
$$\int^0_0$$   anything$$= 0$$

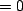
we get the result,

$$\frac{\rho_{se}(t)}{dt}=\frac{1}{i\hbar}[H_i(t),\rho_{se}(0)]-\frac{1}{\hbar^2}\int_0^t \left[H_i(t),[H_i(t'),\rho_{se}(t')]\right]$$ (3.3)