


Next: The Integration
Up: Detailed Derivation of the
Previous: Assumptions
We assume the system can be modeled with the Hamiltonian,
![$\displaystyle H_{s}=\hbar \omega a^{\dagger}a, \ \ \ [a,a^{\dagger}]=1$](img10.png) |
(2.1) |
Separately we assume that there exists a bath which can be
modeled with the Hamiltonian,
![$\displaystyle H_{b}=\sum_i \hbar \omega_i b_i^{\dagger}b_i, \ \ \ [b_i,b_k^{\dagger}]=\delta_{ik}$](img11.png) |
(2.2) |
Finally, as stated before, the interaction of the bath and system is
taken in the form of
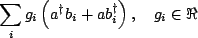 |
(2.3) |
The total Hamiltonian is,
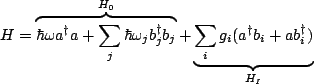 |
(2.4) |
We assume uncertainty in the preparation of states, so we switch to the
density operator regime. We call the density operator corresponding to our bath coupled system 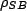 (S: Single original oscillator; B: Environment) where the individual density operators can be retrieved via a trace, i.e.
(S: Single original oscillator; B: Environment) where the individual density operators can be retrieved via a trace, i.e.
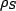 |
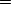 |
 Trace over environment states Trace over environment states |
|
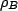 |
 |
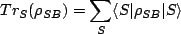 Trace over local states Trace over local states |
|
The dynamics of the system evolve as (Liouville equation),
![$\displaystyle i\hbar\frac{d\rho_{SE}}{dt}=[H,\rho_{SE}]$](img20.png) |
(2.5) |
We commit a unitary transform to simplify this equation as follows (the so-called interaction picture). It can be shown that,
![$\displaystyle \exp(\alpha A)B\exp(-\alpha A)= B + \alpha[A,B] + \frac{\alpha^2}{2!}[A,[A,B]] + \cdots$](img21.png) |
(2.6) |
Furthermore, from the premises of Quantum Mechanics, it is legitimate to commit
transforms of the type,
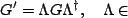 Unitary Unitary |
(2.7) |
These so called similarity transformations preserve rank, determinant, trace, and eigenvalues.
We let,
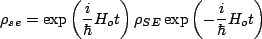 |
(2.8) |
We take the time derivative and find,
![$\displaystyle \frac{d\rho_{se}}{dt}=\frac{i}{\hbar}[H_o,\rho_{se}]-\frac{i}{\hb...
...(\frac{i}{\hbar}H_o t\right)[H,\rho_{SE}]\exp\left(-\frac{i}{\hbar}H_o t\right)$](img24.png) |
(2.9) |
From equation 2.6, since
and
![$ [H_o,H_o] = 0$](img26.png) ,
,
![$\displaystyle \frac{d\rho_{se}}{dt}=-\frac{i}{\hbar}[H_i, \rho_{se}]$](img28.png) |
(2.10) |
where 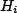 is the transform of
is the transform of 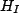 and can be calculated as follows. We know that,
and whereas
and can be calculated as follows. We know that,
and whereas
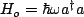 , equation 2.6 gives
, equation 2.6 gives
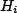 can be calculated in this fashion for both the
can be calculated in this fashion for both the
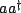 and the multiple set
and the multiple set
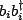 ,
where it is thus now trivial to find that,
,
where it is thus now trivial to find that,
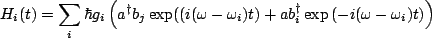 |
(2.11) |
If we now define
we can simplify to
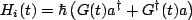 |
(2.12) |
Since the bath is in equilibrium, we can construct 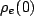 easily. Let
easily. Let
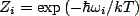 . Then the probability that one
mode (i) of the field is excited with n photons is
. Then the probability that one
mode (i) of the field is excited with n photons is
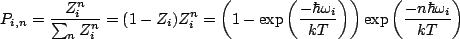 |
(2.13) |
The density matrix for this mode is then
To simplify this further, we imagine a three states system in which we can represent
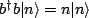 as,
for example letting
as,
for example letting 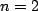 ,
The above sum could then be written,
We recover the matrix, and so we can write just as well,
,
The above sum could then be written,
We recover the matrix, and so we can write just as well,
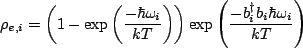 |
(2.15) |
By the rules of probability, the density operator for the entire bath becomes,
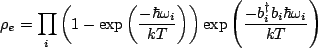 |
(2.16) |
By our assumptions, this is the state of the bath for all time, and so we will not write this as a function of time. The form 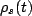 will take will be much more complicated, and it is the purpose of this report to derive the differential equation defining its time evolution.
will take will be much more complicated, and it is the purpose of this report to derive the differential equation defining its time evolution.



Next: The Integration
Up: Detailed Derivation of the
Previous: Assumptions
Timothy Jones
2006-10-11
![]() (S: Single original oscillator; B: Environment) where the individual density operators can be retrieved via a trace, i.e.
(S: Single original oscillator; B: Environment) where the individual density operators can be retrieved via a trace, i.e.
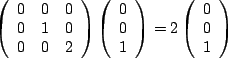
![$\displaystyle 0\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\left[\begin{ar...
...y}{c}0\\ 0\\ 1\end{array}\right)\left[\begin{array}{ccc}0&0&1\end{array}\right]$](img51.png)