


Next: Construction of the Hamiltonian
Up: Detailed Derivation of the
Previous: Detailed Derivation of the
We begin by outlining the assumptions which enable the canonical
derivation of the master equation. Our general assumption is that
our system is a harmonic oscillator (
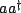 ) which interacts
with a bath of oscillators (
) which interacts
with a bath of oscillators (
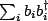 ). Specifically:
). Specifically:
- We assume that the energy spectrum of the bath of oscillators is spaced
tightly enough relative to its overall domain, i.e.
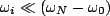 such that the approximation
such that the approximation
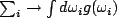 , where
, where
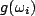 is the density of states of the reservoir, is a
physically acceptable mathematical assumption.
is the density of states of the reservoir, is a
physically acceptable mathematical assumption.
- Related to the previous assumption, we assume that the bath is large
enough and in a state of equilibrium such that any perturbations caused by the individual system on the bath
is negligible. This is to say, the future state of the system-bath density
operator is determined by its current state, and is not a function of the
history of the bath (that is, we assume
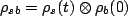 ).This is the Markoffian assumption.
).This is the Markoffian assumption.
- We assume the rotating wave approximation regime. The interaction of
the bath and system will have terms such as
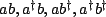 . The lowering-lowering and raising-raising coupling has
a much slower varying contribution to the state of the system, and so are
excluded to give the interaction Hamiltonian
. The lowering-lowering and raising-raising coupling has
a much slower varying contribution to the state of the system, and so are
excluded to give the interaction Hamiltonian
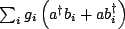 where
where 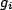 is a real coupling constant. Obviously, one
must be certain the system one models can be simplified as such in order to
apply the general master equation.
is a real coupling constant. Obviously, one
must be certain the system one models can be simplified as such in order to
apply the general master equation.



Next: Construction of the Hamiltonian
Up: Detailed Derivation of the
Previous: Detailed Derivation of the
Timothy Jones
2006-10-11