

Next: 15-96
Up: Energy I: Week 2
Previous: 15-79.
The point of this problem is to give some practice in evaluating the
two constants 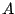 and
and 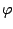 given an initial condition. We have
the equations
given an initial condition. We have
the equations
from which we can evaluate the initial conditions. Now, one condition
is that 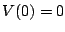 , which yields
, which yields
so either 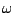 ,
, 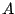 , or
, or 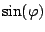 is zero. Our oscillator
would be boring if either the first two were true, so we go with the
last one, which means either
is zero. Our oscillator
would be boring if either the first two were true, so we go with the
last one, which means either 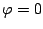 OR
OR 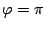 . Make sure
you realize the angle can have multiple values!
. Make sure
you realize the angle can have multiple values!
Next, we use the position condition
Since we (usually) take 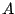 to be a positive quantity, we need
to be a positive quantity, we need
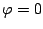 , since otherwise
, since otherwise 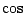 comes out negative. But,
comes out negative. But,
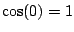 , so
, so 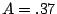 .
.
Note, we could have used 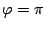 and
and 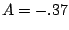 . Either is fine.
. Either is fine.
Dan Cross
2006-10-03
![]() and
and ![]() . Either is fine.
. Either is fine.