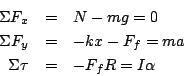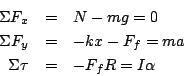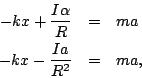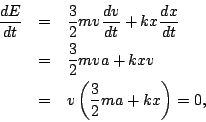

Next: About this document ...
Up: Energy I: Week 2
Previous: 15-87.
Like all problems that change the basic setup, we need to go back to
FBD's before we can apply our spring results. The forces acting are
gravity, spring, normal, and friction (rolls without slipping!). So,
taking our center of torque to be the center of the wheel, we get
where 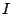 is the moment of inertia and
is the moment of inertia and 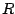 the radius. Note that
acceleration to the right means clockwise rolling, or negative angular
acceleration, so
the radius. Note that
acceleration to the right means clockwise rolling, or negative angular
acceleration, so 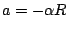 . Eliminating
. Eliminating 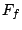 from the second two
equations yields
from the second two
equations yields
or, after collection of terms and rearranging
Thus we have an equation of the form
but with
that is, we still have simple harmonic motion, but the rolling inertia
makes our `effective mass' larger. In this case 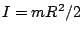 , so
, so
It is straightforward to show the period is as advertised at this point.
The total energy any point is the sum of three terms:
Notice that 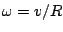 , so that
, so that
Now,
and the time derivative of 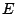 is
is
where the last follows since 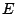 is constant. This equation is
identical to the one derived above.
is constant. This equation is
identical to the one derived above.


Next: About this document ...
Up: Energy I: Week 2
Previous: 15-87.
Dan Cross
2006-10-03