

Next: 15-87.
Up: Energy I: Week 2
Previous: 15-59.
What we have to note here is that the condition of the cars before the
bottom one breaks away enables us to determine the spring constant of
the rope since the system was in static equilibrium. The component of
weight along the incline of the 3 cars balances the spring force, so
Newton's Second Law gives us
where 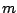 is the mass of one car and
is the mass of one car and 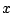 the stretch of the spring, so
solving for
the stretch of the spring, so
solving for 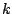 yields
yields
which allows us to determine the frequency. But, be careful, only two
of the cars oscillate, so the mass now is 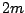 !
!
Now, for the amplitude we note that the breaking free of the bottom
car set our initial conditions: the string is stretched by
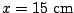 and the initial velocity is zero. When the bottom one breaks
free our forces are unbalanced so the net force up the incline is
still
and the initial velocity is zero. When the bottom one breaks
free our forces are unbalanced so the net force up the incline is
still
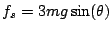 , but the gravitation part downward is only
, but the gravitation part downward is only
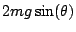 . The net force is then
. The net force is then 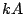 (since we oscillate
about the new equilibrium position), so
(since we oscillate
about the new equilibrium position), so
Another way to do this part is to to write 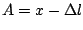 , and find
the stretch of the spring from its unstretched length as we did
before. Both expressions should agree.
, and find
the stretch of the spring from its unstretched length as we did
before. Both expressions should agree.


Next: 15-87.
Up: Energy I: Week 2
Previous: 15-59.
Dan Cross
2006-10-03
![]() and the initial velocity is zero. When the bottom one breaks
free our forces are unbalanced so the net force up the incline is
still
and the initial velocity is zero. When the bottom one breaks
free our forces are unbalanced so the net force up the incline is
still
![]() , but the gravitation part downward is only
, but the gravitation part downward is only
![]() . The net force is then
. The net force is then ![]() (since we oscillate
about the new equilibrium position), so
(since we oscillate
about the new equilibrium position), so
![]() , and find
the stretch of the spring from its unstretched length as we did
before. Both expressions should agree.
, and find
the stretch of the spring from its unstretched length as we did
before. Both expressions should agree.