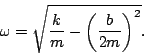

Next: 15-79.
Up: Energy I: Week 2
Previous: Vertical Springs
The solution for a damped spring can be written in the form
where we have
When written in this form it is obvious that the non-damped spring is
written the same way with 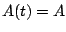 is time-independent. In any case,
part a) refers to the amplitude only - the
is time-independent. In any case,
part a) refers to the amplitude only - the 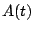 . Thus, since
. Thus, since
we have
There are a few ways to consider the next part. If there are 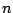 oscillations then the angle has changed by an mount
oscillations then the angle has changed by an mount 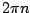 , that is
, that is
Which yields
expressed in various ways (note that we don't need 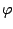 ). Thus
all we need is
). Thus
all we need is 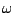 for a damped system, which is given by
for a damped system, which is given by
Dan Cross
2006-10-03
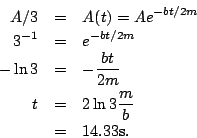
![]() oscillations then the angle has changed by an mount
oscillations then the angle has changed by an mount ![]() , that is
, that is