

Next: 15-59.
Up: Energy I: Week 2
Previous: Energy I: Week 2
Vertical Spring problems are more complicated than their horizontal
counterparts, but they're really just a more general case. In fact,
we can look at springs on any angle of an incline for a continuous
range of problems. We begin our analysis with a spring hanging
without any mass. The spring length (now unstretched) is 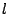 . Now,
suppose we hang a mass on the spring and then gently let it stretch
the spring until equilibrium is achieved, and suppose this stretching
to have length
. Now,
suppose we hang a mass on the spring and then gently let it stretch
the spring until equilibrium is achieved, and suppose this stretching
to have length 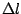 . Then Newton's Second Law says that:
. Then Newton's Second Law says that:
(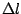 is negative) which gives us our expression for the stretch
of the spring from the old equilibrium position
is negative) which gives us our expression for the stretch
of the spring from the old equilibrium position
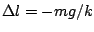 .
Notice that the new equilibrium position of the system (no force) is
different from the old one (no stretch in the spring). The two
are the same only when a spring is horizontal.
.
Notice that the new equilibrium position of the system (no force) is
different from the old one (no stretch in the spring). The two
are the same only when a spring is horizontal.
Now, suppose the spring is further stretched from the new equilibrium
position, so that the total stretching is 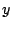 . Then we have
. Then we have
where we have set
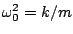 . Note that we don't know the
angular frequency yet - this was simply an algebraic replacement.
This last equation suggests that we define a new quantity
. Note that we don't know the
angular frequency yet - this was simply an algebraic replacement.
This last equation suggests that we define a new quantity
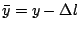 , since derivatives annihilate constants. A quick
calculation gives the equation
, since derivatives annihilate constants. A quick
calculation gives the equation
which is the usual equation for harmonic motion. Now we can conclude
that 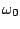 is in fact the angular frequency, and the mass
executes oscillations with respect to the new equilibrium position.
is in fact the angular frequency, and the mass
executes oscillations with respect to the new equilibrium position.
Thus, the total effect of having a vertical spring is to shift the
equilibrium position down by the amount 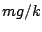 , so that at equilibrium
the spring is under tension and has energy. Make sure you remember
this when computing energies.
, so that at equilibrium
the spring is under tension and has energy. Make sure you remember
this when computing energies.
Finally, note that if we have a spring on an incline, the equilibrium
position is determined by
where 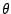 is incline angle. Thus we see that the separation
between the new and old equilibrium depends on that angle and goes to
zero as the angles does, which is a horizontal spring. Here the two
positions are degenerate (the same).
is incline angle. Thus we see that the separation
between the new and old equilibrium depends on that angle and goes to
zero as the angles does, which is a horizontal spring. Here the two
positions are degenerate (the same).


Next: 15-59.
Up: Energy I: Week 2
Previous: Energy I: Week 2
Dan Cross
2006-10-03
![]() . Then we have
. Then we have
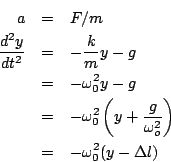
![]() , so that at equilibrium
the spring is under tension and has energy. Make sure you remember
this when computing energies.
, so that at equilibrium
the spring is under tension and has energy. Make sure you remember
this when computing energies.