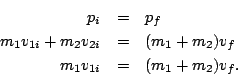15-36.

We know from 28 that the energy and amplitude are directly related: $E=kA^2/2$. Thus, to know the amplitude after the collision we need to know the energy after the collision. That energy has both kinetic and potential contributions in general, so we need to know the position of the spring at the collision (potential) as well as the velocities after the collision (kinetic). Thus the need to find the position and velocity of mass 2 at the given time, and then solve the collision.

However, in the present case we can simplify the analysis because the numbers are nice. First, there are relationship between sine and cosine when the arguments differ by certain phase factors. Whenever you have a phase which is some integer multiple of $\pi/2$, there may be a possible simplification. In this case we have the relationship

$$\cos(\omega t +\pi/2)=-\sin(\omega t),$$

so that mass 2 starts out at the equilibrium position at $t=0$.

Next, notice that the period is 20 ms, while the time of impact is 5 ms, or $T/4$. So, the collision happens when mass 2 is at the end of the first quarter of its motion. Since the equation is $-\sin$, the mass will have no speed and will be at position $x=-A=-1$ cm.

First we'll calculate the spring energy, $U=kA^2/2$, but first we need $k$ which is given by

$$k=m_2\omega^2=197\;\textrm{kN/m}.$$

Thus we have $U=9.85\;{\textrm J}$

Next we need to solve the collision, which is inelastic and the initial velocity of the second mass is 0. Thus we have from conservation of momentum:

$$\begin{eqnarray*} p_i &=& p_f \\ m_1v_{1i} + m_2v_{2i}&=& (m_1+m_2)v_f\\ m_1v_{1i} &=& (m_1+m_2)v_f. \end{eqnarray*}$$

This yeilds the value

$$v_f=\frac{m_1}{m_1+m_2}v_{1i}=4\;\textrm{m/s}.$$

This gives a kinetic energy of

$$K=\frac{1}{2}(m_1+m_2)v_f^2=48\;{\textrm J}.$$

Thus the total energy is

$$E=K+U=57.85\;{\textrm J},$$

and then, finally, the amplitude is

$$A=\frac{2E}{k}=2.4\;\textrm{cm}.$$