15-35.

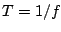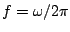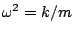The period $T=1/f$, while $f=\omega/2\pi$, and $\omega^2=k/m$. Thus we need to find 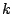$k$. We know 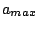$a_{max}$, which can be utilized in a few different ways. The most staightforward is the use the force equation:

$$F=ma=-kx \to F_{max}=ma_{max}=kA.$$

Thus we have

$$k=\frac{m}{A}a_{max}=4\times10^4\;\textrm{N/m}.$$

Doing all of the back substitutions yields $T=3.1\;{\textrm ms}$.

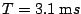Next, we want to find the maximum velocity. Since velocity is the derivative of position we have

$$v(t)=\frac{dx}{dt}=-A\omega\sin(\omega t + \varphi).$$

So, for our maximum value we have

$$v_{max}=A\omega=4\;\textrm{m/s}.$$

We know from 28 that we can use the maximum speed or displacement to calculate the total energy. Choosing displacement, we have

$$E=\frac{1}{2}kA^2=80\;\textrm{mJ}.$$