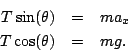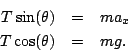

Next: About this document ...
Up: Energy I: Week 1
Previous: 15-36.
Since this problem doesn't involve springs, we'll have
to start from a free body diagram before we can apply the equations we
know. Newtons equations will give:
In the 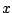 and
and 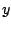 directions respectively. Dividing the top equation
by the bottom gives
directions respectively. Dividing the top equation
by the bottom gives
Next, since we will only discuss small oscillations (larger
oscillations are still harmonic, but are not simple), we will
approximate the tangent by sine (remember this procedure - it is often
used). Thus we have
where 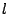 is the length of the pendulum. So if we compare this
equations with the spring equations from before we see that we have
is the length of the pendulum. So if we compare this
equations with the spring equations from before we see that we have
From this expression we can find 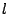 as
as
To find the maximum kinetic energy we will use the velocity if we
remember an equation from circular motion:
so that
and finally


Next: About this document ...
Up: Energy I: Week 1
Previous: 15-36.
Dan Cross
2006-10-18