• Lattice Problems
• Domain Decomposition
• Parallel Implementation
• Elliptic Equation - 1-D Poisson Equation
  • The Model
  • Serial Implementation
  • Parallel Implementation

Lattice Problems

Partial Differential Equations (PDEs) are encountered in virtually all of sciences, engineering disciplines and even in the world of business. We now want to devise a way to implement the solution of these equations on parallel computers. This leads to domain decomposition.

The numerical solution of PDEs almost always imply a numerical lattice to describe the domain over which we seek a solution. A natural (and often the only) way in which to render parallel the task of solving PDEs is to parcel the global domain into sub-domains and to let each processor of the parallel computer handle individual sub-domain; this is domain decomposition.

Note that in solving the so-called trivially parallelizable problems on parallel computers, i.e., the The Mandelbrot Set, the difficulty comes in ensuring load balancing; there is typically little node-to-node message passing. In domain decomposition, just the opposite occurs: minimization of communication is the major hurdle against achieving an efficient parallel code. Load balancing issues occur mostly due to complicated geometry.

We will next review (again) the classification of PDEs and mention the appropriate domain decomposition in each case. We will then describe briefly the implementation of domain decomposition on parallel computers.

Domain Decomposition

PDEs are traditionally classified into three broad categories: elliptic, parabolic and hyperbolic equations. However, from the numerics point of view, PDEs divide into static equations (elliptic) and time dependent equations (parabolic & hyperbolic).

The prototypical elliptic equation is the Poisson equation

where is the field (potential) we look for and the term represents a source term. This equation is encountered in electrostatic, gravitation, ect. The solution is static (time independent) and requires the specification of in a 3-dimension manifold , subject to boundary conditions.

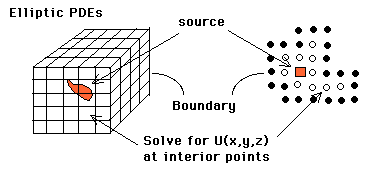
The simplest domain decomposition consists in decomposing the cubic domain into smaller cubes equal in number to the number of processors. The difficulty, as far as load balancing is concerned, arises if the domain is not a cube. Think of what you would do if the domain would be rectangular, or worse of arbitrary shape! The amount of computing to handle each sub-domain obviously depends on the number of lattice points in the sub-domains, an equal number of lattice points in each sub-domain being necessary for load balance...

The hyperbolic and parabolic equations are quite different in that they represent initial value problems. Namely, the wave equation (hyperbolic)

(v=constant is the velocity of the wave propagation) and the diffusion equation (parabolic)

(D is the diffusion coefficient) are such that we ask for what is the value of the field (wave) at a later time t knowing the field at an initial time t=0 and subject to some specific boundary conditions at all times.

In this case, the domain decomposition applies to the space variables. The time evolution is essentially sequential, is obtained from , which can not be parallelized. This is also true in obtaining a solution of ODEs.

Parallel Implementation

Domain decomposition is implemented on a parallel computer by letting each processor handle a sub-domain (or at most a few sub-domains). Therefore the choice of these sub-domains becomes crucial in obtaining good performance. The strategy in choosing the sub-domains must be guided by the following requirements:

• equal work be done in each sub-domain for load balancing
• node-to-node communication be minimized

The load balancing is often easy to achieve if the geometry of the domain is simple, i.e., cubic, rectangular, ... These domains naturally lead to the same number of lattice points in each sub-domain. If the domain is irregular, the solution is often to "pad" the domain into a regular one, or sometimes to "linearize" the mesh points accessing scheme (done in finite element approaches). This leads to complications and inefficiencies in the implementation; we will not discuss this problem further here. We will assume a simple geometry in what follows.

The minimization of node-to-node communication is the major bottleneck in domain decomposition. The problem stems from the calculation of derivatives in finite-differencing schemes (same applies to finite-element approaches). Consider the 3-point forms for the first and second derivatives of a function:

and

In domain decomposition, each sub-domain is handled by different processors. At the boundary of the sub-domains, the value of the field at the neighbor points on the lattice reside in the local memory of the processors handling the adjacent sub-domains; this requires communication in the calculation of the derivatives.

Each sub-domain (at each time step) therefore becomes a mini-problem to solve; this mini-problem is of the same type as the larger problem, but with boundary conditions defined by the value of the field in the neighbor sub-domains. A two dimension problem looks schematically as:

The implementation of the domain decomposition algorithm only requires the MPI calls we have seen in the previous sections, yet book-keeping considerations can become quite complicated to implement in higher dimension problems.

Elliptic Equation - 1-D Poisson Equation

In this section we solve Poisson equation in 1-D as a simple example of domain decomposition. The distribution of sub-tasks among the processes is typical of what is done in most parallel implementation of parallel equations solvers.

The Model

We will solve the equation

d² j(x) / dx² = s(x)

This function j(x) could represent the electric potential due to a charge distribution s(x), or the steady state temperature profile in the presence of a heat source s(x). The domain is 1-D, x within [ 0 , 1 ]. The boundary conditions are assumed of Dirichlet type, namely j(0) and j(1) are given. In addition, the function j(x) can also be specified on specific points in the interior domain. The source is also given, taken to be a simple gaussian centered at mid-point in what follows.

The domain is discretized on a 1-D numerical lattice, with x_i = (i-1) h, h = 1.0 / ( N - 1 ), and where N is the number of grid points. The Poisson equation is re-written in terms of finite difference form

( j _i+1 - 2 j _i + j _i-1 ) / h² = S _i

This leads to a large set of linear equations to solve for j _i , the field values on the grid, in the domain, keeping j _i fixed at the boundary. This set of equations can be solved by an iterative method, whereby 

j _i  = 1 / 2 ( j _i+1 + j _i-1 - h² S _i)

is iterated "in place" until the changes in j _i become less than some predefined tolerance criteria. An arbitrary guess for j _i  is assumed to start with. The method is stable in that the solution will converge. The old and new values of  j _i are mixed to accelerate the convergence, leading to the "over relaxation" scheme. The accuracy of the solution is second order in h.

Serial Implementation

The code poisson_1d.c implements the above scheme. The steps in the code are:

• Initialize the numerical grid
• Provide an initial guess for the solution
• Set the boundary values & source term
• Iterate the solution until convergence
• Output the solution for plotting

The code, poisson_1d.c,  is compiled and executed

        gcc poisson_1d.c -lm -o poisson_1d

        poisson_1d 5000 100 > solution_1d.dat

where 5000 and 100 are the (arbitrary) maximum number of iterations and number of grid points respectively. The code stops once good convergence ( parameter EPS ) is obtained. Use gnuplot to graph the solution.

Note:

• The "chi" parameter which implements the over-relaxation approach is chosen arbitrarily for simplicity (see "Numerical Recipes" for an optimum choice)
• The exact solution of the 1-D Poisson equation with no source is a straight line. This is almost what is obtained at small x where the source term is small.
• The use of "malloc" for memory management is encouraged here to prepare for the parallel version.
• The code is written in the simplest possible way, with no function, to simplify reading it. Functions will be introduced in the parallel implementation.

Parallel Implementation

Domain decomposition consists in dividing the original grid among the processes with an equal number of grid points in each process for good load balance. If the number of grid points does not divide equally among the processes, the extra grid points are distributed one each to a subset of processors as indicated schematically in the following figure.

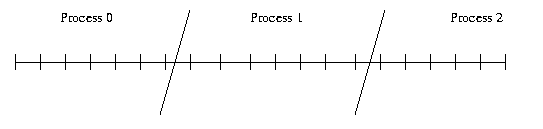
This results in the following arrangement on each processor

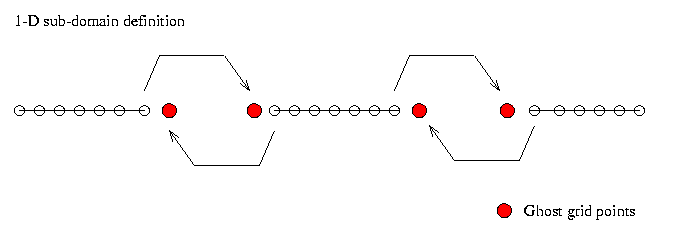
The calculation of the derivative terms in finite difference scheme requires the field values at neighbor grid points to be known. Therefore, the value of the field at the artificial boundary between sub-domain must be transmitted between the neighbor processes as indicated in the figure. This must be done at each iteration during the calculation, leading to much transmission.

There are many issues involved in setting up a parallel code to solve PDEs. Here are some of the most important ones:

• Minimize communication.
  • Done by choosing the geometry well - for instance in 2-D a stripe or a "square" geometry can be chosen. The stripe case is definitely easier to program and can make use of an arbitrary number of processors. The square topology for the sub-domain is restricted to n₁ x n₂ number of processors. Questions left for the reader to ponder: which topology leads to less perimeter values to transmit at each iteration? And how about transmission startup overhead costs?
    
• The parallel implementation puts all processes on the same footing - no master-slave concepts here!
  
• If parts of the calculation needs repeating on different processes to save communication time, let it be so. This is done in the code for the grid and sub-domain calculations whose results are fast to compute and needed in all processes.
  
• Communication blocking must be avoided.
  • This may results if all processes are requested to send the field variables for the GHOST positions at the same time, and then subsequently requested to receive the values. Think about it:  the send will block until the messages are received, yet the processes won't receive until the sends are completed. 
  • This problem is solved by using an odd-even scheme of transmission. This is shown schematically as
    • even process
      • send - to right (top) neighbor
      • recv - from left (bottom) neighbor
      • send - to left (bottom) neighbor
      • recv - from right (top) neighbor
    • odd processes
      • recv - from left (bottom) neighbor
      • send - to right (top) neighbor
      • recv - from right (top) neighbor
      • send - to left (bottom) neighbor
        
• Keeping track of the grid indices in each sub-domain and which processes contain neighbor sub-domains can be a difficult task, specially in higher dimensional problems and when complicated geometries are involved. Heads up in the coding!
  
• The arrays containing the field variables in the sub-domains must include extra space for the "GHOST" values. 
  • The 1-D parallel code uses "large" arrays space for the fields in the sub-domains. This choice makes it possible for the index range in the sub-domain to follow that of  the global domain, i.e., imin to imax, and second to easily allow the inclusion of the "GHOST" values in the array,  i.e., dimension imin-1 to imax+1. But it wastes memory space.
    
• Calculation of the changes in the fields in the entire domain from an iteration to the next requires global operations
  •  In this context MPI provides global operation routines. We use MPI_Allreduce( ) which allows the calculation of the overall maximum (MPI_MAX) among the values of a single variable in the different processes and to have this value known to all processes.
    
• The real time and memory saving in using parallel computers to solve PDEs is only evident in higher dimensions where the amount of calculation per iteration is large compared to the overhead in transmission introduced by the parallel implementation. For instance, do not be surprised by the fact that the 1-D serial code is faster to run than the parallel code.
  
• Will the parallel code give exactly the same answer as the scalar code? In the current implementation, the code gives the same answer only to the accuracy specified for the convergence, i.e., EPS in the code. Namely, as written, the serial and parallel code do not give exactly, i.e., within machine accuracy, the same solution. This is due to the order in which the calculation is done, the GHOST values being the "old" field instead of the "updated" ones. The solution to this problem requires a change in the algorithm. Heads up -- not all algorithms transcribe exactly to a parallel environment.

The flowchart of the parallel code is given below:

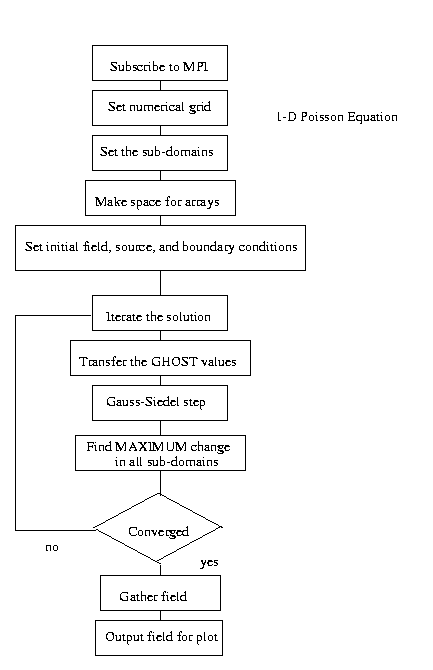
The parallel code, poisson_parallel_1d.c,  is compiled and executed via the same commands as the serial code:

        mpicc  poisson_parallel_1d.c   -lm -o poisson_parallel1d

        mpiexec -np 4 poisson_parallel_1d  5000  100 |  > data_parallel