


Next: Gamma, Digamma, Polygamma Functions
Up: The legal way I:
Previous: Bernoulli Numbers
To start,
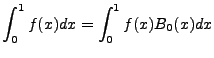 |
(2.10) |
It is also obvious that
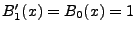 so that,
so that,
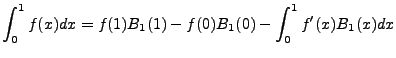 |
(2.11) |
Carrying on and seeing that
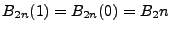 and
and
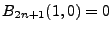 , we would find,
, we would find,
![$\displaystyle \int^1_0f(x)dx = \frac{1}{2}[f(1)+f(0)] - \sum^{q}_{p=1} \frac{1}...
...}[f^{(2p-1)}(1)-f^{(2p-1)}(0)] + \frac{1}{(2q)!}\int^1_0 f^{(2q)}(x)B_{2q}(x)dx$](img25.png) |
(2.12) |
The transform
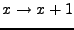 ,
,
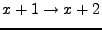 ,etcetera, yields,
,etcetera, yields,
root
2006-09-15
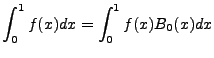
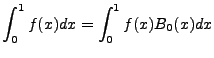
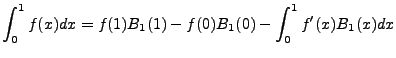
![$\displaystyle \int^1_0f(x)dx = \frac{1}{2}[f(1)+f(0)] - \sum^{q}_{p=1} \frac{1}...
...}[f^{(2p-1)}(1)-f^{(2p-1)}(0)] + \frac{1}{(2q)!}\int^1_0 f^{(2q)}(x)B_{2q}(x)dx$](img25.png)
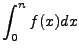
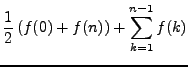
![$\displaystyle -\sum^{q}_{p=1} \frac{1}{(2p)!}B_{2p}[f^{(2p-1)}(1)-f^{(2p-1)}(0)] + \frac{1}{(2q)!}\int^1_0 B_{2q}(x)\sum^{n-1}_{\chi=0}f^{(2q)}(x+\chi)dx$](img31.png)