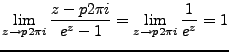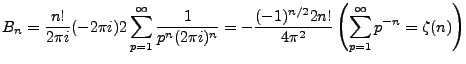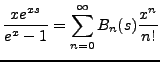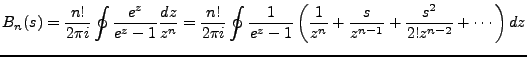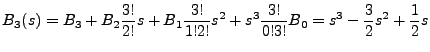Next: Euler-Maclaurin Integration Formula
Up: The legal way I:
Previous: The legal way I:
We can define a set of numbers, the so called Bernoulli Numbers, via the equation,
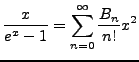 |
(2.1) |
Complex analysis allows us to extract the 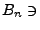
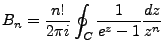 |
(2.2) |
We can construct a contour which avoids the central pole (wrapping over the positive
real axis, around a clockwise infinitesimal circle centered at the origin, and back along
the positive real axis to rejoin the the main contour of clockwise orientation. We then
have,
![$\displaystyle B_n = \frac{n!}{2\pi i}(-2\pi i)\sum_{p} Res[\pm p2\pi i]$](img11.png) |
(2.3) |
where
![$\displaystyle Res(f;z_0)=\lim_{z\rightarrow z_0}\frac{1}{(m-1)!}\frac{d^{m-1}}{dz^{m-1}}[(z-z_0)^mf(z)]$](img12.png) |
(2.4) |
With an application of l'Hopital's rule,
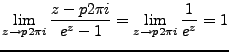 |
(2.5) |
Thus we note that the odd residues beyond one will cancel each other out
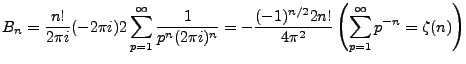 |
(2.6) |
For example,
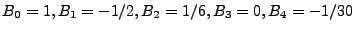 , and so on.
Bernoulli functions are derived in the same way, defined by
, and so on.
Bernoulli functions are derived in the same way, defined by
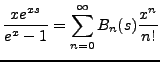 |
(2.7) |
This is easily solved by expanding the extra 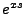 factor and relating the results to the previous
results for the Bernoulli numbers, i.e.,
factor and relating the results to the previous
results for the Bernoulli numbers, i.e.,
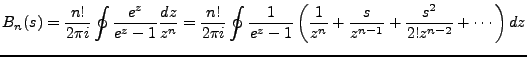 |
(2.8) |
For example,
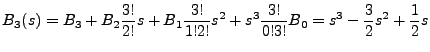 |
(2.9) |



Next: Euler-Maclaurin Integration Formula
Up: The legal way I:
Previous: The legal way I:
root
2006-09-15
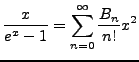
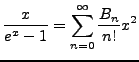
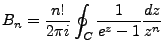
![$\displaystyle B_n = \frac{n!}{2\pi i}(-2\pi i)\sum_{p} Res[\pm p2\pi i]$](img11.png)
![$\displaystyle Res(f;z_0)=\lim_{z\rightarrow z_0}\frac{1}{(m-1)!}\frac{d^{m-1}}{dz^{m-1}}[(z-z_0)^mf(z)]$](img12.png)