


Next: The Preperation of Rydberg
Up: The Aufbau Principal, Kramers
Previous: Kramer's Relation and the
A change in energy levels for a Rydberg atom in a circular
state must obey selection rules so that
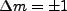 or 0, and
or 0, and
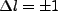 . Thus an atom in a Rydberg state under guarded environmental condtions
can only transition as
. Thus an atom in a Rydberg state under guarded environmental condtions
can only transition as
Thus a Rydberg atom approximates a two-level system.
We demonstrate the theory behind elementary selection rules with a simple example.
A two-state system in the presence of puturbing Hamiltonian can be described as,
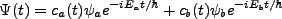 |
(3.1) |
Its evolution is described by
from which we have,
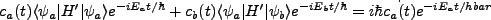 |
(3.2) |
Rejoining convention and writing
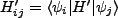 ,
,
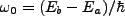 , and assuming (as is warented in
the experiments we discuss) that the diagonal of the perturbing part of the Hamiltonian is zero, we can obtain a
set of equations for the prefactors,
, and assuming (as is warented in
the experiments we discuss) that the diagonal of the perturbing part of the Hamiltonian is zero, we can obtain a
set of equations for the prefactors,
Following [4] we consider a basic hydrogen atom in the 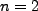 state in an electric field so that
state in an electric field so that
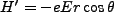 .
As we showed in a previous compendium, the wave functions for hydrogen,
.
As we showed in a previous compendium, the wave functions for hydrogen, 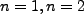 , are
, are
The perturbation matrix is simple in that all but one of these will be even
in
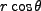 , so the perturbation matrix (
, so the perturbation matrix (
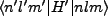 )
will have all zero elements except
)
will have all zero elements except
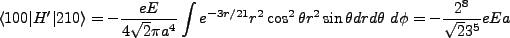 |
(3.5) |
| |
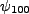
|
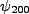
|
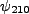
|
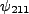
|
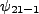
|
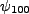
|
0 |
0 |
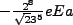
|
0 |
0 |
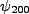
|
0 |
0 |
0 |
0 |
0 |
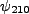
|
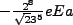
|
0 |
0 |
0 |
0 |
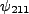
|
0 |
0 |
0 |
0 |
0 |
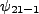
|
0 |
0 |
0 |
0 |
0 |
Thus we see that under this perturbation, the
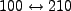 levels are ``selected'
and we have an approximate two-state system under the right conditions (ideal).
levels are ``selected'
and we have an approximate two-state system under the right conditions (ideal).
In general, we can derive selection rules for m and l transitions. In the case of m, we
consider that ![$ [L_z,z]=0$](img111.png) so that
so that
![$\displaystyle 0=\langle n'l'm'\vert[L_z,z]\vert nlm\rangle=(m'-m)\langle n'l'm'\vert z\vert nlm\rangle$](img112.png) |
(3.6) |
That
![$ [L_z,x]=i\hbar y$](img113.png) gives,
gives,
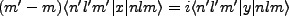 |
(3.7) |
Finally,
![$ [L_z,y]=-i\hbar x$](img115.png) gives,
gives,
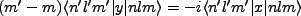 |
(3.8) |
Thus
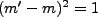 or
or
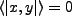 .
For the
.
For the 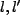 case, it can be shown that
case, it can be shown that
From this we can show that
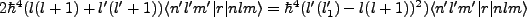 |
(3.9) |
Rewriting
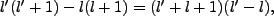
and
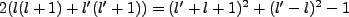
We thus conclude that 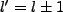 and
and
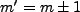 or
or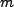



Next: The Preperation of Rydberg
Up: The Aufbau Principal, Kramers
Previous: Kramer's Relation and the
tim jones
2007-04-09
![]() , so the perturbation matrix (
, so the perturbation matrix (
![]() )
will have all zero elements except
)
will have all zero elements except
![]() so that
so that