Timothy Jones
we have
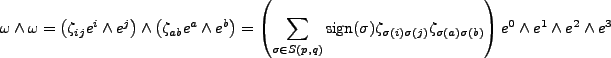
| Combination | Sign |
| (0,1)(2,3) | + 1 |
| (0,2)(1,3) | -1 |
| (0,3)(1,2) | +1 |
| (1,2)(0,3) | +1 |
| (1,3)(0,2) | -1 |
| (2,3)(0,1) | +1 |
One explicates this and finds,
We might stop here, and simply search for a combination of coefficients so that the above product is not zero, but we must note that the combination is suggestive of Sarrus's scheme in that the
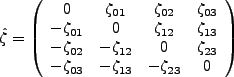
![\includegraphics[width=5cm]{triangle.ps}](img7.png)
The mechanisms of the wedge product prefactor coupling and the determinant formation are suggestively similar. It is one of the greatest sadnesses in mathematics that Sarrus's scheme does not extend beyond three dimensional arrays. The determinant is instead found by Laplace's theorem, as
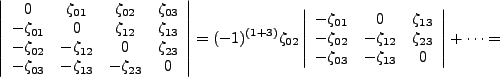
Does this then suggest that
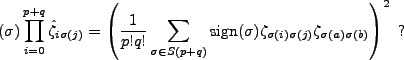
At this point, we investigated further and found a reference on Wikipedia (of course) regarding the Pfaffian in relation to the wedge product. We also consulted with our colleague Daniel Cross who confirmed that this was indeed the right path. Further investigation brought us into consideration of the extensive work on determinants by Thomas Muir1, and we wish to take the reader along this path to show how indeed the above equation is true via Muir's work.
A determinant can be defined by use of minors, e.g.
If we switch
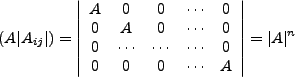
Thus the determinant of the adjucate is the determinant of ![]() .
Now to get to our next point, we have found the fastest path is a short
proof by S. Parameswaran published in The American Mathematical Monthly
(Vol. 61, No. 2. (Feb., 1954), p. 116). We recreate the proof in whole here.
For n even, we define the determinant of our matrix to be,
.
Now to get to our next point, we have found the fastest path is a short
proof by S. Parameswaran published in The American Mathematical Monthly
(Vol. 61, No. 2. (Feb., 1954), p. 116). We recreate the proof in whole here.
For n even, we define the determinant of our matrix to be,

Then

We now rejoin Muir where we write this generically as,
For zero-axial skew-symmetric determinants, the left side simplifies to
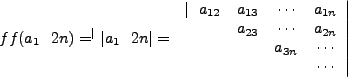 |
This confirms our suspicion, and generically we write2:
An example of such a matrix would be the electromagnetic variable matrix seen in electrodynamics3.