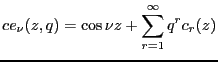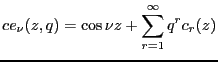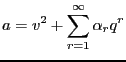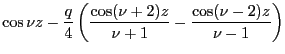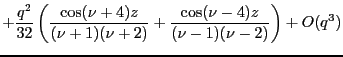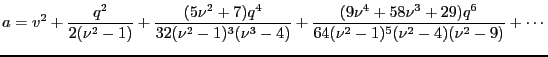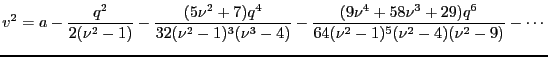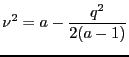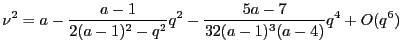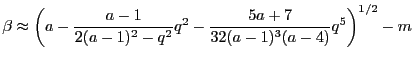Next: Mathieu & Maple, forever
Up: Technical details
Previous: Integral order
Now we suppose solutions of the form
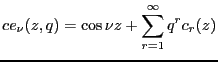 |
(5.5) |
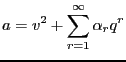 |
(5.6) |
Quoting again our references [4,3], the above procedure may be applied to find,
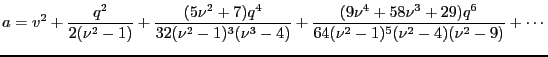 |
(5.8) |
The latter can be rewritten,
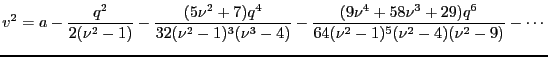 |
(5.9) |
A first approximation is 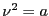 . Putting this into the
. Putting this into the 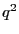 coefficient gives a second
approximation,
coefficient gives a second
approximation,
And repeating the process gives
Finally we note that
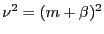 (the integral and fractional component), we have the approximation
(the integral and fractional component), we have the approximation
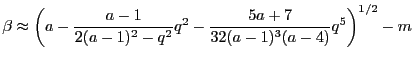 |
(5.10) |
The cosine functions have sine equivalents which we have not included for the sake of brevity.
These formulations are not uncommon in the literature, though for obvious reasons the previous
derivations were presented in fuller context as they seem to be the preferred method of dealing
with the Mathieu equation. But alas, after presenting so many ways of
looking at Mathieu's equation, like Pandora's box, last out is hope.



Next: Mathieu & Maple, forever
Up: Technical details
Previous: Integral order
tim jones
2008-07-07