| (3.1) | |||
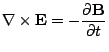 |
(3.2) | ||
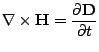 |
(3.3) |
| (3.1) | |||
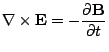 |
(3.2) | ||
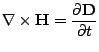 |
(3.3) |
In this environment, ![]() and
and
![]()
The simplicity of these four equations begs for even further simplification, whereby we introduce the vector potential,
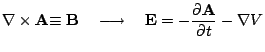
There are many ways to fit these equations while maintaining the validity
of the Maxwell equations. The coulomb potential suffices and is preferrable
due to its simplicity:
![]() ,
, ![]() . The identity
. The identity
![]() coupled with our previous assertation and equation 3 above yield
coupled with our previous assertation and equation 3 above yield
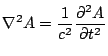 |
(3.4) |
We will quantize this centralized magnetic potential. To completely specify the field we would have to describe its values for all points in space; it is customary to develop the quantization in a theoretical cube, and then let the volume of the cube expand to infinity to accomplish a full discription.
Our derivation can consider standing or plane waves. The case of standing waves is quicker. We assume the magnetic potential has a solution of form
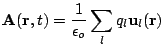 |
(3.5) |
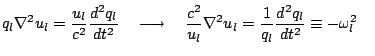 |
(3.6) | ||
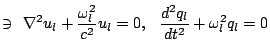 |
(3.7) |
The energy stored by our electromagnetic field is
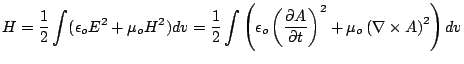 |
(3.8) |
We assume via our target solution that our spatial modes will have the orthogonality
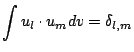 |
(3.9) |
Using this orthogonality, we have
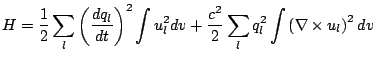 |
(3.10) |
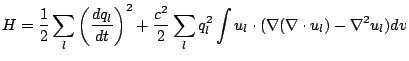 |
(3.11) |
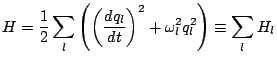 |
(3.12) |
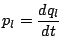 |
(3.13) | ||
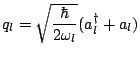 |
(3.14) | ||
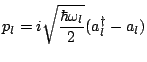 |
(3.15) |
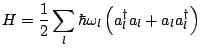 |
(3.16) |