

Next: About this document ...
Up: TDEC 115 - Week
Previous: Formulas and Concepts
I will start with the junction and two loop (left and right) equations:
Note that 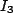 is the current through the capacitor, so
is the current through the capacitor, so
Thus, we want to end up with a equation involving only  and
and 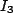 . Thus we solve the first equation for
. Thus we solve the first equation for  and substitute into the second equation to get
and substitute into the second equation to get
which we then solve for 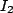 to get
to get
Now we substitute this into the third equation to remove 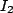 , which, after collecting terms, becomes
, which, after collecting terms, becomes
At first glance this looks entirely intractable, but notice that everything besides 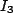 and
and  is a constant! So, let's turn them into the more simplistic (and suggestive) constants:
is a constant! So, let's turn them into the more simplistic (and suggestive) constants:
which yields the equation
which should look very familiar. Since this is exactly the usual RC loop equation, we immediately obtain the solution
in terms of our primed quantities. Thus the capacitor sees an effective EMF given by 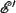 , and this arrangement is known as a voltage divider (something you'll see a lot of in a circuits class...); and the capacitor sees an effective resistance given by
, and this arrangement is known as a voltage divider (something you'll see a lot of in a circuits class...); and the capacitor sees an effective resistance given by 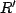 , which is written as
, which is written as 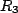 in parallel with the series combination
in parallel with the series combination 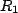 and
and 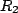 , which is the equivalent resistance if we remove the EMF! Thus, this is the justification for the statements made earlier.
, which is the equivalent resistance if we remove the EMF! Thus, this is the justification for the statements made earlier.
Finally, let us find the voltage 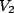 . This quantity is the same as the voltage through the parallel branch that includes the capacitor, thus we have
. This quantity is the same as the voltage through the parallel branch that includes the capacitor, thus we have
and we have
so putting things together we obtain
Note that 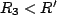 so the term in the parenthesis is positive, and the function increaes in time as we know it must. Now, if we substitute in our values we have
so the term in the parenthesis is positive, and the function increaes in time as we know it must. Now, if we substitute in our values we have
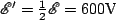 and
and 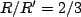 , and thus
, and thus
which yields the limiting values
Moreover, the functional form of 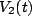 has exponential dependence, just as we assumed.
has exponential dependence, just as we assumed.


Next: About this document ...
Up: TDEC 115 - Week
Previous: Formulas and Concepts
Daniel Cross
2006-09-18
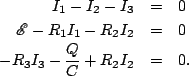
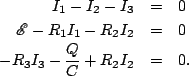
![]() and
and ![]() is a constant! So, let's turn them into the more simplistic (and suggestive) constants:
is a constant! So, let's turn them into the more simplistic (and suggestive) constants:
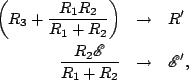
![]() . This quantity is the same as the voltage through the parallel branch that includes the capacitor, thus we have
. This quantity is the same as the voltage through the parallel branch that includes the capacitor, thus we have
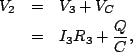
![\begin{eqnarray*}
V_2(t) &=& \frac{R_3}{R'}\mathscr{E}'\left(e^{-t/R'C}\right)+ ...
...thscr{E}'\left[1-\left(1-\frac{R_3}{R'}\right)e^{-t/R'C}\right],
\end{eqnarray*}](img48.png)