

Next: HRW 27-53
Up: TDEC 115 - Week
Previous: TDEC 115 - Week
Now we expand our discussion of circuits by including the capacitor into the mix. To write down our circuit equations we need to know how to handle a capacitor. A capacitor has a voltage across its plates equal to 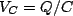 . Now we need to know which sign to use. If the current flows into a plate, that plate should accumulate positive charge, and so should have the higher potential. Thus we have
. Now we need to know which sign to use. If the current flows into a plate, that plate should accumulate positive charge, and so should have the higher potential. Thus we have
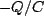
- If you go through a capacitor in the direction of the current you go down in potential by
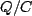 .
.
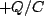
- If you go through a capacitor opposite the current you go up in potential by
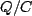 .
.
Figure 1:
Voltage rules for capacitors in a circuit.
|
|
This next key idea has to do with the short (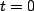 ) and long (
) and long (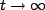 ) time behavior of a capacitor in a circuit.
) time behavior of a capacitor in a circuit.
- An uncharged capacitor acts like a short circuit since
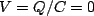
- A fully charged capacitor acts like an open circuit since
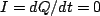 .
.
Thus the short and long time problems reduce to the ones earlier involving only batteries and resisters since the capacitor no longer explicitly appears. We will typically utilize these statements by first writing down the general loop and junction equations, but then simplifying them with  or
or 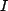 set to
set to 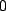 .
.
Next, we note the solutions to the differential equations for simple 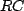 circuits. For charging we have the loop equation
circuits. For charging we have the loop equation
where we have set 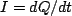 , which has solution
, which has solution
where
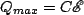 is the maximum charge on the capacitor (at
is the maximum charge on the capacitor (at 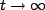 ) and
) and 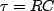 is the time constant, whose value determines how long the capacitor takes to charge.
is the time constant, whose value determines how long the capacitor takes to charge.
For discharging we have the loop equation
where we have set 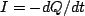 , which has solution
, which has solution
where 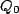 is the initial charge value. Note that the current is found in both cases by differentiation. Know also what the graphs of these exponential functions look like. This is important!
is the initial charge value. Note that the current is found in both cases by differentiation. Know also what the graphs of these exponential functions look like. This is important!
Figure 2:
Graphs of the exponential functions in dimensionless quantities.
|
Finally, if it is needed, when you have a complicated RC circuit (one with many resisters), we can still solve the equations by writing down the 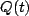 equation, but making making the following replacements:
equation, but making making the following replacements: 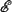 becomes the maximum total EMF seen by the capacitor (ie, the voltage drop across the branch with the capacitor when the current there is zero); and
becomes the maximum total EMF seen by the capacitor (ie, the voltage drop across the branch with the capacitor when the current there is zero); and 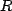 becomes the total resistance in series with the capacitor (ie, mentally remove all EMFs and reduce the resulting resister network to just one in series with
becomes the total resistance in series with the capacitor (ie, mentally remove all EMFs and reduce the resulting resister network to just one in series with 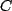 ). We will justify this with an example:
). We will justify this with an example:

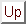

Next: HRW 27-53
Up: TDEC 115 - Week
Previous: TDEC 115 - Week
Daniel Cross
2006-09-18
![]() ) and long (
) and long (![]() ) time behavior of a capacitor in a circuit.
) time behavior of a capacitor in a circuit.
![]() circuits. For charging we have the loop equation
circuits. For charging we have the loop equation