

Next: 37-5
Up: Energy I - Week
Previous: Space-Time Diagrams
In this problem, the father wants take a very speedy trip, so that his
daughter left on earth will age 40 more years than he does. But he
ages 4 years during the trip, so she must age 44 years total. More
explicitly, if we let  be the daughters initial age and
be the daughters initial age and  her
final age, we have
her
final age, we have
The we have
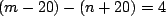 , that is, the father ages
, that is, the father ages  years.
Simplifying the expression yields
years.
Simplifying the expression yields  , so that the daughter ages
44 years.
, so that the daughter ages
44 years.
On the diagram below (fig.4) the daughter stays on earth, so her line is just
the 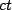 axis. She is at
axis. She is at  at every time
at every time  . The father moves
with constant speed away from earth for 2 years in his frame (
. The father moves
with constant speed away from earth for 2 years in his frame ( ) and then abruptly turns around and heads back to earth at
the same constant speed for another 2 years (in his frame). The
daughter ages 44 years in her frame during the whole trip, or 22 years
on the father's way out and 22 more on his way back.
) and then abruptly turns around and heads back to earth at
the same constant speed for another 2 years (in his frame). The
daughter ages 44 years in her frame during the whole trip, or 22 years
on the father's way out and 22 more on his way back.
Figure 4:
Space-time diagram for 37-4.
|
|
So, our event of interest is when the father turns around in his
trip. We know both the  and
and  coordinates of this point, so
lets see if we can find the corresponding
coordinates of this point, so
lets see if we can find the corresponding 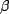 . The Lorentz time
transformation says that
. The Lorentz time
transformation says that
so that we need to know  , that is, how far the daughter measures
the father to have traveled before turning around. Well, if the
father moves with constant speed
, that is, how far the daughter measures
the father to have traveled before turning around. Well, if the
father moves with constant speed  and for a time
and for a time  , then
the distance traveled is
, then
the distance traveled is
We could also determine this from the second Lorentz transform
equation noting that the  coordinate of when the father turns
around is exactly 0 because one is always at rest in their own frame
of reference (the origin of his coordinate system is always centered
on him). Then we have
coordinate of when the father turns
around is exactly 0 because one is always at rest in their own frame
of reference (the origin of his coordinate system is always centered
on him). Then we have
which immediately gives  since
since  .
.
So, now we can substitute for  giving
giving
or
which is the equation for time dilation: since  the time
the time  measured in the stationary frame is larger than the time
measured in the stationary frame is larger than the time  measured
in the moving frame by the factor
measured
in the moving frame by the factor  . Note that we made the
substitution
. Note that we made the
substitution
 . (Show this is true.)
. (Show this is true.)
Now we just substitute in for gamma and solve for 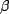


Next: 37-5
Up: Energy I - Week
Previous: Space-Time Diagrams
Daniel Cross
2006-11-15
![]() , that is, the father ages
, that is, the father ages ![]() years.
Simplifying the expression yields
years.
Simplifying the expression yields ![]() , so that the daughter ages
44 years.
, so that the daughter ages
44 years.
![]() axis. She is at
axis. She is at ![]() at every time
at every time ![]() . The father moves
with constant speed away from earth for 2 years in his frame (
. The father moves
with constant speed away from earth for 2 years in his frame (![]() ) and then abruptly turns around and heads back to earth at
the same constant speed for another 2 years (in his frame). The
daughter ages 44 years in her frame during the whole trip, or 22 years
on the father's way out and 22 more on his way back.
) and then abruptly turns around and heads back to earth at
the same constant speed for another 2 years (in his frame). The
daughter ages 44 years in her frame during the whole trip, or 22 years
on the father's way out and 22 more on his way back.
![]() and
and ![]() coordinates of this point, so
lets see if we can find the corresponding
coordinates of this point, so
lets see if we can find the corresponding ![]() . The Lorentz time
transformation says that
. The Lorentz time
transformation says that
![]() giving
giving

![]()
