Next: The Simpson Rule Up: Integrals Previous: Integrals
The simplest methods follow from assuming that each strip under the curve is a rectangle based on the function value at the left or at the right of each strip. However, intuition tells us that this will give a very inaccurate value for the area since we are approximating the underlying function by straight line segments.
A more accurate form follows if we assume that each strip is of the
shape of a trapezoid.
The area of such a trapezoidal shaped strip is
| (5) |
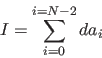 |
(6) |
The advantage of using the simple form of
![]() is that the exact integral is easily analytically performed
is that the exact integral is easily analytically performed
| (7) |
| (8) |
Can you derive this result?
What is the percent error in the Trapezoidal rule area as compared to the exact one?
2015-01-05