



Next: Experimental Example of Superposition
Up: Is Quantum Decoherence the
Previous: What is Decoherence?
Contents
Unique to wave theories is the concept of superposition of states.
Indeed, the interference of states is often used as a defining characteristic
of quantum systems such that the destruction of a pre-existing interference
pattern is identified with a transition into the classical realm (``the
appearance of the classical world'' [15]).
In demonstrating the mathematics of decoherence, the simplest
system we could possibly start with must entail at least two states capable
of superposition. We consider a simple harmonic oscillator in the state,
 |
(2.1) |
Generically, we define  as an eigenvalue of the annhilation
operator state of the oscillator,
as an eigenvalue of the annhilation
operator state of the oscillator,
 |
(2.2) |
These so called coherent states represent a quantum system which is
very close to being in a classical state (see appendix).
Let us ignore, for now, the need for normalization (or if preferred, assume the system
is normalized as is). It is well known that the Hamilton for such a system is simply
given by
The unitary evolution of this wave function is,
 |
(2.3) |
Note that
It can be written,
 |
(2.4) |
The density matrix is
 |
(2.5) |
To get a clear picture of the interference this superposition entails, we can take a look at this
system in the coordinate representation. We have that,
We can thus obtain,
 |
(2.6) |
Let
 . Then we can write,
. Then we can write,
 |
(2.7) |
The latter follows from the fact that the two cross terms will be conjugates, and for any complex number z,
 . We can partition
this function into real and imaginary parts as follows. We write
. We can partition
this function into real and imaginary parts as follows. We write
We note that
Thus,
It is now conventional to chose a simple case in which
 and
and
 ,
,
 |
(2.9) |
The convenient  form makes calculation of the cross term easy, and it is,
form makes calculation of the cross term easy, and it is,
 |
(2.10) |
 |
(2.11) |
If Decoherence is to bring us into the classical realm, 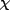 must be destroyed.
Let us be more explicit here. Equation 2.11 gives us only partial information, i.e. the probabilities for any given position q'.
To represent the density matrix in proper form, we need integrate over all positions, i.e. the density matrix is
must be destroyed.
Let us be more explicit here. Equation 2.11 gives us only partial information, i.e. the probabilities for any given position q'.
To represent the density matrix in proper form, we need integrate over all positions, i.e. the density matrix is
 |
(2.12) |
A classical density matrix would not have off diagonal terms. The total probability of finding the particle in one state or the other
is given by
 |
(2.13) |
Experimental demonstration of the effect of superposition has made much progress in the last decade, and we
discuss one such example in the next section.




Next: Experimental Example of Superposition
Up: Is Quantum Decoherence the
Previous: What is Decoherence?
Contents
tim jones
2007-04-11
![]() as an eigenvalue of the annhilation
operator state of the oscillator,
as an eigenvalue of the annhilation
operator state of the oscillator,
