

Next: 37-33
Up: Energy I - Week
Previous: 37-13
This problem discusses how the measurements of the speed of an object as
made by two different observers are related. Since nothing can go
faster than light as seen by any observer, we know the the
relationship isn't going to be the same as in Galilean relativity. In
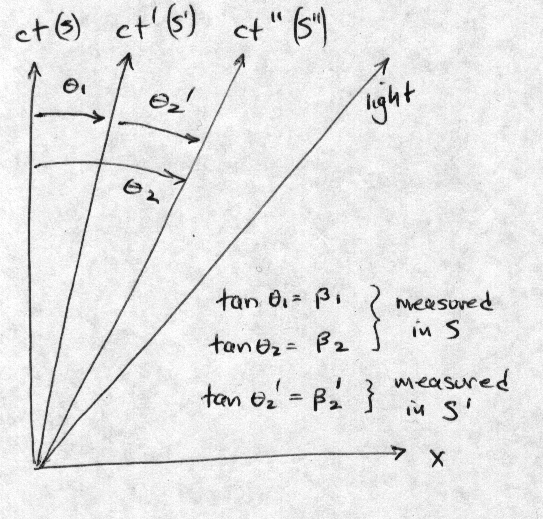
the diagram below (fig.8) we have time axis from 3 different observers. The
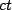 axis is the 'stationary' observer,
axis is the 'stationary' observer, 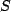 . The
. The 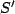 observer (
observer (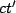 axis) moves with speed
axis) moves with speed 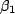 as measured by S, and the observer
as measured by S, and the observer
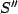 (
(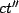 axis) moves with speed
axis) moves with speed 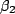 as measured in S. We
will then let
as measured in S. We
will then let 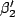 be the speed of
be the speed of 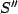 as measured by
as measured by 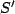 .
.
Figure 8:
Space-time diagram for 37-30.
|
|
Note that we have labeled the angles between the time axis in the
figure. We have
Now, remember from the section on space-time diagrams that the angle
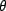 is related to the velocity parameter
is related to the velocity parameter 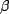 by
by
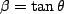 . So, lets take the tangent of the above equation
relating the various angles and try to convert it all to
. So, lets take the tangent of the above equation
relating the various angles and try to convert it all to 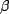 's:
's:
where we used a trig identity from the back of the book and in the
last line substitute each 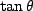 for the corresponding
for the corresponding 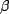 .
This is the formula for converting speed measurements of a third object
(here
.
This is the formula for converting speed measurements of a third object
(here 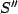 ) between two frames (
) between two frames (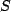 and
and 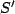 ).
).
The data given is
That is, we know the speed of the second frame as measured by the
first, and the speed of the third as measured by the second. So we
can use the above formula to find 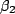 , the speed of the third as
measured by the first. We have
, the speed of the third as
measured by the first. We have
The classical counter part to this formula is the numerator only
which gives a velocity greater than that of light. We then see that
it is the denominator in our formula which ensures that no velocity
can ever be measured to be greater than light.
In the next part the third object is moving in the opposite direction
as seen by 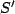 , that is,
, that is, 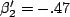 now. But he calculations
are the same:
now. But he calculations
are the same:
while the classical calculation is
and agrees more closely with the relativistic calculation since the
speed is not as close to the speed of light.


Next: 37-33
Up: Energy I - Week
Previous: 37-13
Daniel Cross
2006-11-15
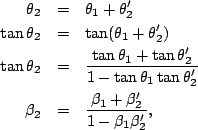
![]() , that is,
, that is, ![]() now. But he calculations
are the same:
now. But he calculations
are the same: