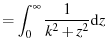 |
(66) | |
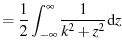 |
(67) | |
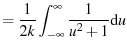 |
(68) |
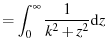 |
(66) | |
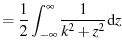 |
(67) | |
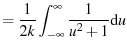 |
(68) |
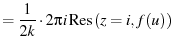 |
(69) | |
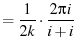 |
(70) | |
| (71) | ||
| (72) |
We will show that for any
![]()
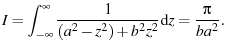 |
(73) |
First we note that
![]() like
like ![]() for
for ![]() ,
and that
,
and that ![]() is even, so
is even, so
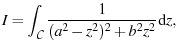 |
(74) |
Because the denominator is of the form ![]() , we can factor it
into
, we can factor it
into
![]() like so
like so
| (75) |
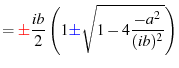 |
(76) | |
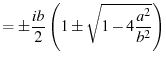 |
(77) | |
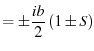 |
(78) |
To determine the nature and locations of the roots, consider the following
cases (in order of increasing ![]() ).
).
In the overdamped case
![]() and
and ![]() ,
so
,
so ![]() is purely imaginary, and
is purely imaginary, and
![]() .
For any
.
For any ![]() , we have
, we have ![]() , so
, so
![]() .
Thus, there are two single poles in the upper half plane (
.
Thus, there are two single poles in the upper half plane (![]() ),
and two single poles in the lower half plane (
),
and two single poles in the lower half plane (![]() ).
).
In the critically damped case ![]() , so
, so
![]() ,
and we have double poles at
,
and we have double poles at
![]() .
.
In the underdamped case ![]() is purely imaginary,
so
is purely imaginary,
so ![]() is complex, with
is complex, with ![]() in the 2
in the 2
![]() quarter,
and
quarter,
and ![]() in the 1
in the 1
![]() quarter.
The other two simple poles,
quarter.
The other two simple poles, ![]() and
and ![]() , are in the
3
, are in the
3
![]() and 4
and 4
![]() quarters respectively.
quarters respectively.
Our contour
![]() always encloses the poles
always encloses the poles ![]() .
We will deal with the simple pole cases first,
and then return to the critically damped case.
.
We will deal with the simple pole cases first,
and then return to the critically damped case.
Our factored function ![]() is
is
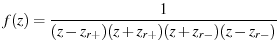 |
(79) |
Applying eq. 63 and 64 we have
| (80) | ||
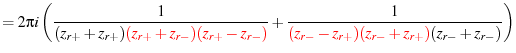 |
(81) | |
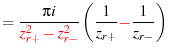 |
(82) | |
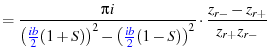 |
(83) | |
![$\displaystyle = \frac{\textcolor{Blue}{-4}\pi i / \textcolor{Blue}{b^2}}{ (1+2S...
...[(1-S) - (1+S)] } { \left(\frac{ib}{2}\right)^{\textcolor{Red}{2}} (1+S)(1-S) }$](img192.png) |
(84) | |
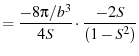 |
(85) | |
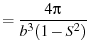 |
(86) | |
![$\displaystyle = \frac{ 4\pi }{ b^3 [1 - (1-4\frac{a^2}{b^2})]}$](img195.png) |
(87) | |
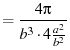 |
(88) | |
| (89) |
Our factored function ![]() is
is
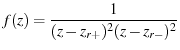 |
(90) |
Applying eq. 63 and 65 we have
| (91) | ||
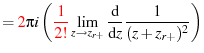 |
(92) | |
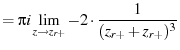 |
(93) | |
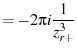 |
(94) | |
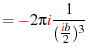 |
(95) | |
| (96) | ||
| (97) |