

Next: 3 Theoretical power spectral
Up: cantilever_calib
Previous: 1 Overview
Subsections
To find 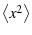 , the raw photodiode voltages
, the raw photodiode voltages 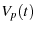 are
converted to distances
are
converted to distances 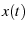 using the photodiode sensitivity
using the photodiode sensitivity
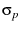 (the slope of the voltage vs. distance curve of data taken
while the tip is in contact with the surface) via
(the slope of the voltage vs. distance curve of data taken
while the tip is in contact with the surface) via
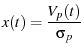 |
(5) |
Rather than computing the variance of 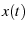 directly, we attempt to
filter out noise by fitting the spectral power density (
directly, we attempt to
filter out noise by fitting the spectral power density (
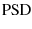 ) of
) of
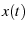 to the theoretically predicted
to the theoretically predicted
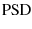 for a damped harmonic
oscillator (eq. 53)
for a damped harmonic
oscillator (eq. 53)
where
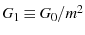 ,
, 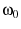 , and
, and 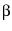 are used as the
fitting parameters (see eqn.s 53). The variance of
are used as the
fitting parameters (see eqn.s 53). The variance of
 is then given by eq. 59
is then given by eq. 59
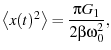 |
(8) |
which we can plug into the equipartition theorem
(eqn. 1) yielding
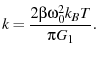 |
(9) |
From eqn. 61, we find the expected value of 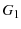 to be
to be
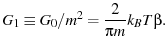 |
(10) |
In order to keep our errors in measuring 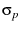 seperate from
other errors in measuring
seperate from
other errors in measuring
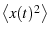 , we can fit the voltage
spectrum before converting to distance.
, we can fit the voltage
spectrum before converting to distance.
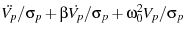 |
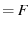 thermal thermal |
(11) |
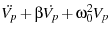 |
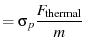 |
(12) |
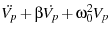 |
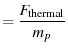 |
(13) |
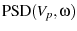 |
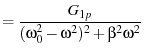 |
(14) |
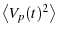 |
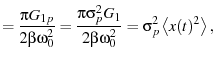 |
(15) |
where
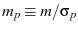 ,
,
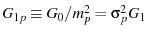 .
Plugging into the equipartition theorem yeilds
.
Plugging into the equipartition theorem yeilds
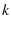 |
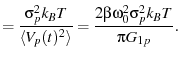 |
(16) |
From eqn. 10, we find the expected value of 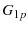 to be
to be
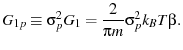 |
(17) |
Note: the math in this section depends on some definitions from
section 3.
As yet another alternative, you could fit in frequency
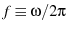 instead of angular frequency
instead of angular frequency 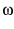 . But we
must be careful with normalization. Comparing the angular frequency
and normal frequency unitary Fourier transforms
. But we
must be careful with normalization. Comparing the angular frequency
and normal frequency unitary Fourier transforms
from which we can translate the
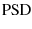
The variance of the function 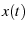 is then given by plugging into
eqn. 34 (our corollary to Parseval's theorem)
is then given by plugging into
eqn. 34 (our corollary to Parseval's theorem)
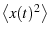 |
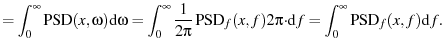 |
(22) |
Therefore
where
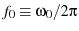 ,
,
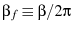 , and
, and
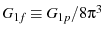 . Finally
. Finally
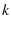 |
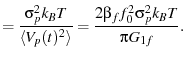 |
(26) |
From eqn. 10, we expect 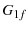 to be
to be
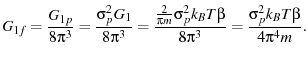 |
(27) |


Next: 3 Theoretical power spectral
Up: cantilever_calib
Previous: 1 Overview
Download cantilever_calib.pdf
View the source files or my
.latex2html-init configuration file
2 Methods
Copyright © 2009-10-12, W. Trevor King
(contact)
Released under the GNU Free Document License, Version 1.2 or later
Drexel Physics
![]() , the raw photodiode voltages
, the raw photodiode voltages ![]() are
converted to distances
are
converted to distances ![]() using the photodiode sensitivity
using the photodiode sensitivity
![]() (the slope of the voltage vs. distance curve of data taken
while the tip is in contact with the surface) via
(the slope of the voltage vs. distance curve of data taken
while the tip is in contact with the surface) via
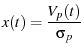
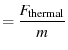
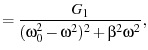
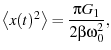
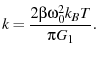
![]() to be
to be
![]() seperate from
other errors in measuring
seperate from
other errors in measuring
![]() , we can fit the voltage
spectrum before converting to distance.
, we can fit the voltage
spectrum before converting to distance.
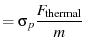
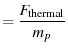
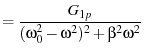
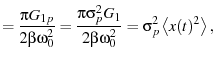
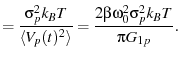
![]() to be
to be
![]() instead of angular frequency
instead of angular frequency ![]() . But we
must be careful with normalization. Comparing the angular frequency
and normal frequency unitary Fourier transforms
. But we
must be careful with normalization. Comparing the angular frequency
and normal frequency unitary Fourier transforms
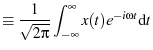
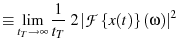
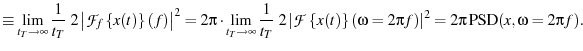
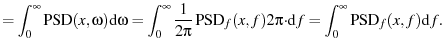
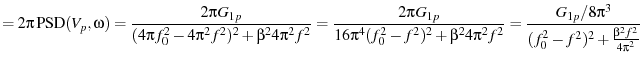
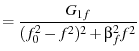
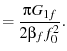
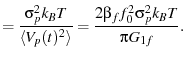
![]() to be
to be