• Elliptic Equation - 2-D Poisson Equation
  • The Model
  • Serial Implementation
  • Parallel Implementation
• Red and Black algorithm

Elliptic Equation - 2-D Poisson Equation

The Model

We will solve the equation

We solve for the function u(x,y) in a 2-D domain, x in [0,1] and y in [0,1]. The boundary conditions are assumed of Dirichlet type, namely u(0,y), u(1,y), u(x,0), and u(x,1) are given. In addition, the function u(x,y) can also be specified on specific points in the interior domain. 

The source S(x,y) is taken to be a simple (displaced) Gaussian in what follows for simplicity.

The domain is discretized on a 2-D numerical lattice, with x_i = (i-1) h, y_j = (j-1)h, and h = 1.0/(N-1). N is the number of grid points in both directions. The Poisson equation is re-written in finite difference form:

This leads to a large set of linear equations to solve for the field values u_i,j on the grid within the domain, keeping u_i,j   fixed at the boundary. This set of equations can be solved by an iterative method, whereby 

is iterated "in place" until the changes in u_i,j  

become less than some predefined tolerance criteria. An arbitrary guess for u_i,j  is assumed to start with. The method is stable, i.e.,  the solution will converge. 

The old and new values of  u_i,j  are mixed to accelerate the convergence, leading to the "Successive Over Relaxation" scheme. 

The accuracy of the solution remains second order in h.

Serial Implementation

The code poisson_2d.c implements the above scheme. The steps in the code are:

• Initialize the numerical grid
• Provide an initial guess for the solution
• Set the boundary values & source term
• Iterate the solution until convergence
• Output the solution for plotting

The code is compiled and executed via

        gcc poisson_2d.c -lm -o poisson_2d

        ./poisson_2d  N    N_x   N_y   > "./out.data"        

where N, N_x and N_x are the (arbitrary) maximum number of iterations and number of grid points - image size - respectively. Good numbers to use could be ( 10000 - 300 - 300 ). 

Upon completion, the file out.data (arbitrary name) contains the potential values in a format consistent with gnuplot.

The code stops once good convergence ( parameter EPS ) is obtained.

Note about the code:

• The "chi" parameter which implements the over-relaxation approach is chosen arbitrarily for simplicity (see "Numerical Receipes" for an optimum choice)
• The code is written in the simplest possible way.
• The code outputs the field values to pipe in plot_image.py for field display

Parallel Implementation

Domain decomposition consists in dividing the original grid among the processes with an equal number of grid points in each process for good load balance. We use here the simplest possible division, i.e., in simple stripes. This results in the following arrangement on each processor.

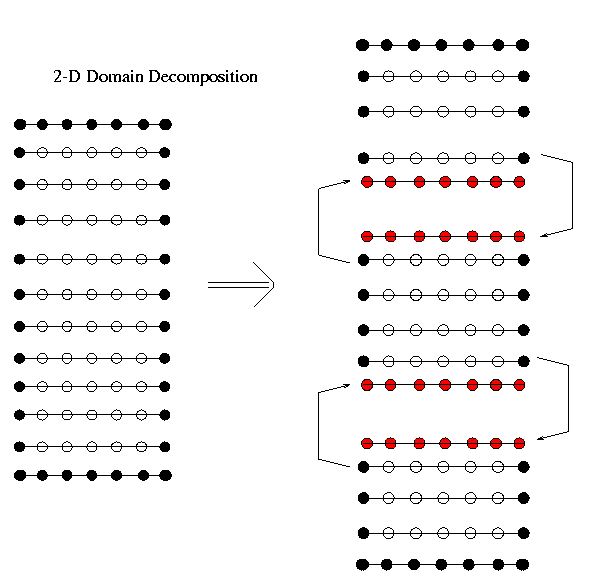
If the number of grid points does not divide equally among the processes, the extra grid points are distributed one each to a subset of processors as indicated schematically in the following figure. 

The domain is divided in stripes which correspond to a split of the first index in the two dimensional arrays containing the fields. This scheme is adopted to facilitate the transmission of the GHOST lines of points. Recall that C stores two dimensional arrays in row fashion; therefore transmitting row ip of the array phi containing jj numbers simply requires

                         MPI_Ssend( &phi[ip][0] , jj, ... )

with no further packing. This is efficient and easy to implement. Note that a FORTRAN programmer would divide the domain in stripes along the second index of the array since FORTRAN stores two dimensional arrays in columns. 

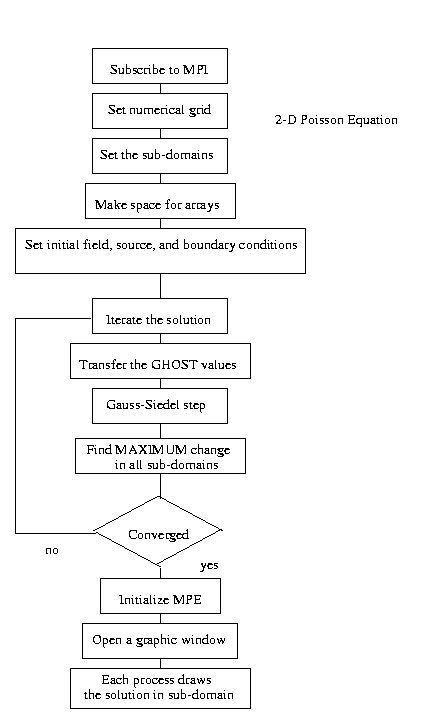
The code should follow very much the approach of the 1-D code. Some functions, like decompose_domain(), could even be borrowed as is since the stripe decomposition is essentially a 1-D domain decomposition. The flowchart below shows the structure that the code should have:

Red and Black algorithm

The parallel and serial implementations of the Poisson equation solver in 2-D as implemented above yield the same results to within the tolerance only. Yet these two implementations are not strictly identical. This stems from the handling of the GHOST lines in the parallel implementation. 

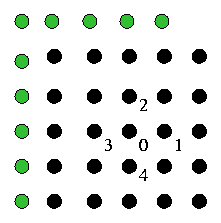
Consider the update of the field at the location marked "0" below. The Gauss-Siedel solution calls for an "in-place" update of the field via the finite difference formula in a systematic sweep of the numerical lattice. This is done via the finite difference formula in 2D. The values of the field at the points "2" and "3" have already been updated if the sweep originates from the upper-left corner of the lattice, while the field at the point "1" and "4" are yet to be updated. 

The sub-domain decomposition requires the transmission of the GHOST line of values at each iteration. This is normally done before each Gauss-Siedel step. The values of the field in these GHOST lines are those of the previous Gauss-Siedel iteration. The value of the field at point "2" below is no longer the updated one. Therefore the parallel implementation is strictly not Gauss-Siedel.

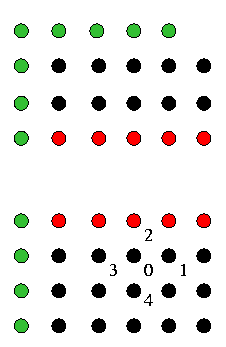
The solution to this problem is to modify the Gauss-Siedel algorithm into the the Red and Black algorithm. In this approach the grid is scanned alternatively on the "Red" then on the "Black" dots. The name is reminiscent of a checker board. 

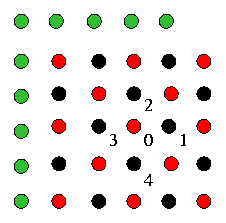
It is clear from the picture that the needed values of the field at points "1", "2", "3", and "4" are the old field values (black) when updating the field at point "0", and vice-versa for any "Red" point. The algorithm then calls fro two subsequent sweep of the lattice alternately on the "Red" and "Black" points. In a parallel implementation, the GHOST lines are exchanged twice at each iteration

• exchange the GHOST lines
• update the "Red" points on the lattice
• exchange the GHOST lines
• update the "Black" points on the lattice

This yields numerically equivalent solutions between the serial and parallel implementations.  This algorithm might be somewhat slower than the strict Gauss-Siedel one.