Numerical Derivatives

Calculating the derivatives of functions is as fundamental as calculating integrals. Numerical approaches are illustrated below.

The figure below illustrates three points in a table listing a function on an equally spaced grid.

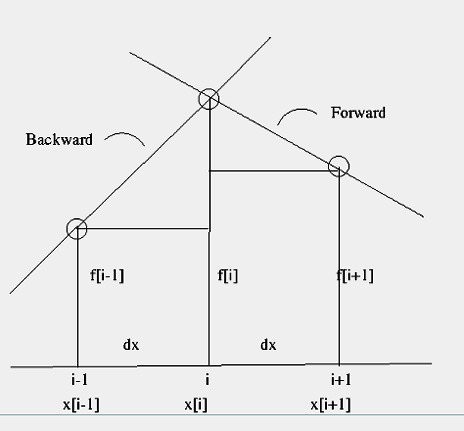
A low order approach follows by using the points $i + 1$ and $i$, the Forward formula. The Backward formula follows the same procedure but is based on the points $i$ and $i-1$. Both of these formulas for the derivative at $i$ yield the same slope in the $limit dx -> 0$ This is found in any calculus textbook. However the numerical approach always implies finite $x$, and therefore not so accurate results.

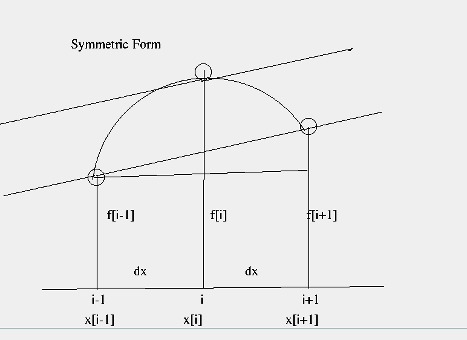
A more accurate way to compute the derivatives is illustrated in the figure below. It uses the function values at points $i + 1$ and $i-1$, It is called the Symmetric form.

The program <a href=../codes/Derivative.cpp> Derivative.cpp</a> reads a tabulated function from a pipe and calculates the derivative on the grid using the three numerical forms, Forward, Backward and Symmetric. The exact derivative of $f(x)$ is also calculated as a reference. It is obvious both graphically and by comparison with the exact answer that the the symmetrical form is the most accurate.

Note that (some of) these formulas do not allow to calculate the derivatives at the first or last points on the grid. Can you analyze why ?

Note also that the calculation of derivatives is intrinsically not very accurate.