Homoclinic Orbit

The Fixed Point at the origin is unstable (maximum of potential). It becomes interesting to study the trajectories initiating near the origin.

There is a special trajectory going through the origin called homoclinic orbit or separatrix. It separates the inner orbits circling the stable Fixed Points (minimum of potential) from the trajectories circling both wells.

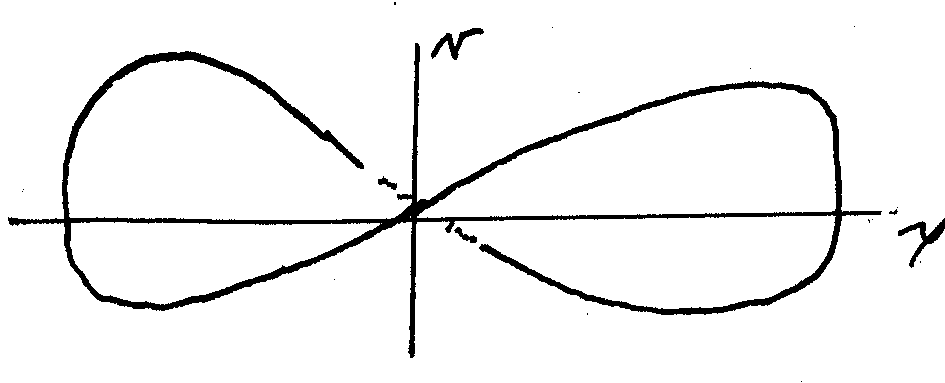
The directions in which the homoclinic orbit spreads out from the origin can be found by analyzing trajectories based on initial conditions distributed on a small circle centered on the origin. The trajectories based on initial conditions near the unstable manifolds will be dragged outward while those based on initial conditions near the stable manifolds will come in toward the unstable point before being dragged outward.

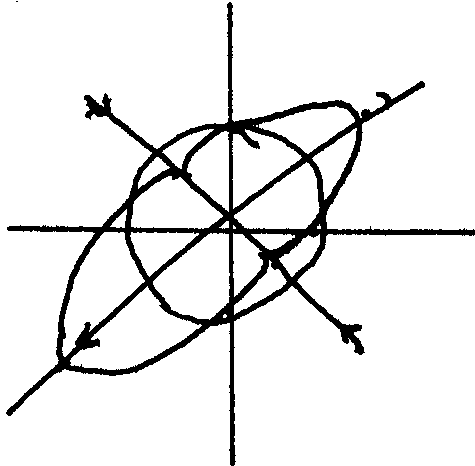
By lengthening the integration time the different trajectories approach the homoclinic orbit.

Exercise #6:

Write a code to generate 100 initial conditions on a small circle around the origin to feed into the ODE solver code. Integrate the ODEs to a small $t_{max}$ until larger values to illustrate the deformation of the circle of initial conditions.

Use the general modular RK4 ODE solver program to solve the Duffing system. Use $\alpha = 1.0$, $\beta = -1$, $\mu = 0.0$, $A = 0.0$ and $\omega = 1$ in the code.

Exercise #7:

Run the integration over larger yet $t_{max}$ to see the shape of the homoclinic orbit.

Dissipative System

Dissipation drives the trajectories in spirals toward either of the two stable Fixed Points located at the minimum of the potential. The homoclinic orbit also spirals toward both stable Fixed Points.

Exercise #8:

Use the general modular RK4 ODE solver program to solve the Duffing system. Use $\alpha = 1.0$, $\beta = 1$, $\mu = 0.1$, $A = 0.0$ and $\omega = 1$ in the code.

Feed the initial conditions generated via the 2 wells setup code in the ODE solver code.

Plot a phase space portrait of the solutions.

Exercise #9:

Superpose the homoclinic orbit generated via initial conditions on a circle onto the graph above