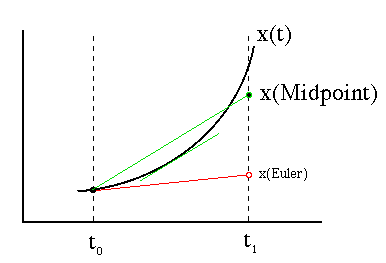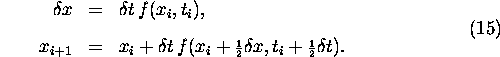The Euler & Mid-point Methods
The simplest possible integration scheme for the initial-value problem is as follows. Given the differential equation
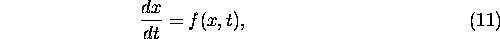
starting with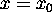 
at time t = 0,
subdivide time into a lattice
by
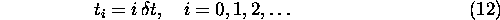
(the equation numbers come from a more extensive document from which
this page is taken) where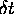 
is some suitably short time interval. Then, knowing
,
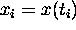we integrate the system forward in time according to the prescription
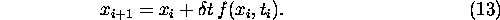
Geometrically, as illustrated in the figure below, we are simply ``following the tangent'' to the solution curve during the timestep, then redetermining the slope of the surve and taking the next step along the new tangent.
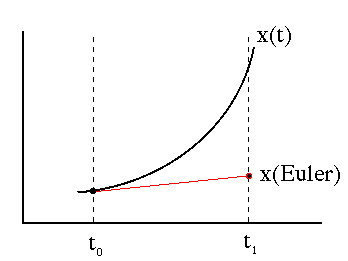
This scheme is known as the Euler method. It generalizes trivially to the case where x is a vector. The program euler.c is a simple implementation of the one-dimensional case. The equation it solves is dx / dt = x .
The Euler method has the undeniable advantage of simplicity.
Unfortunately, it is not very accurate--the error at the end of a
timestep is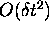 
, and this can
mount up over the duration of a real calculation. Much worse is the
fact that the Euler method can become unstable under certain
circumstances--an undesirable property of any integrator. This
instability can be controlled by careful timestep control. However,
Euler's low order and the fact that the next simplest method--the
Midpoint method--is stable, more accurate, and only marginally more
complicated to program, mean that the Euler method is never
used in real calculations.
The Euler method uses a one-sided estimate of the derivative to
advance the system from time i to time i+1. We would do
better if we could use a centered estimate--that is, if we know
the derivative at the center of the interval, at time `` i +
1/2''. The reason for this becomes clear if we look at the Taylor
series. Imagine applying the Euler method, but use the derivative at
the mid-point, instead of at the start of the range. We obtain
which is the correct second-order expression (just look at equation
(10), and recall that f = v,
How can we determine the derivative at the mid-point of the
interval? We use Euler! The point is that, even though Euler is not
particularly accurate, when this inaccuracy occurs in the derivative
(which gets multiplied by the timestep), the result is ``accurate
enough'' to produce an overall gain. This ``double'' application of
the Euler scheme to refine the net accuracy is called the
Mid-point method. More formally, we can define the scheme as
follows:
The program midpoint.c implements this scheme
for the same function as the earlier euler.c.
The Mid-point Method
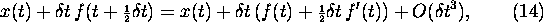
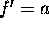). We
have gained an extra order in accuracy just by evaluating the
derivative at a different time! Once again, it is easiest to see
what's going on geometrically:
