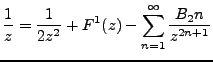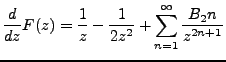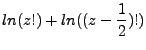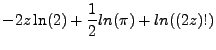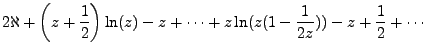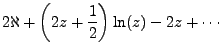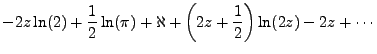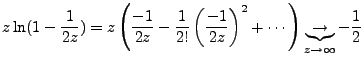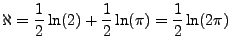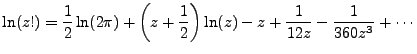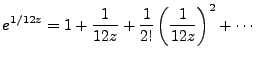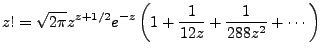Next: Bibliography
Up: A collected derivation of
Previous: Beta Function and the
The application of the Euler-Maclaurin Integration Formula to the function
and recalling the Polygamma function, we know that,
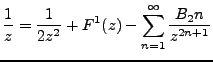 |
(4.1) |
Which is to say,
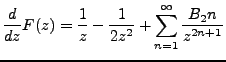 |
(4.2) |
Which is also to say, after some integration,
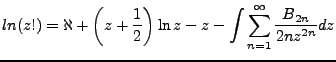 |
(4.3) |
We can solve for 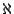 by using the Legendre duplication formula in 4.3 and taking
by using the Legendre duplication formula in 4.3 and taking
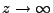 .
In this sense, we will proceed but ignore all pieces on the order of
.
In this sense, we will proceed but ignore all pieces on the order of 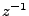 or less, so that,
or less, so that,
Here we must detail the disappearance of the 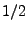 :
:
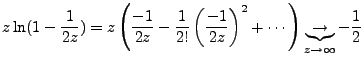 |
(4.4) |
Now we can cancel out what we may cancel out and separate
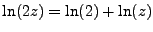 , finally taking the limit of z,
, finally taking the limit of z,
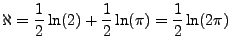 |
(4.5) |
At last, we have
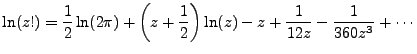 |
(4.6) |
Finally, by noting for example that,
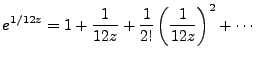 |
(4.7) |
we also have,
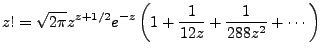 |
(4.8) |



Next: Bibliography
Up: A collected derivation of
Previous: Beta Function and the
root
2006-09-15