Next: The legal way I:
Up: A collected derivation of
Previous: A collected derivation of
As a physicist, one often disregards the formalities of mathematics which can hinder
ones investigations just as often as they can help. In this section, we present an informal rough derivation
of Stirling's formula.
Consider that
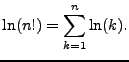 |
(1.1) |
Multiply both sides by 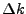 , so,
, so,
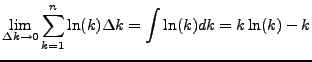 |
(1.2) |
Now of course, in our sum
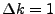 , but the relative size of
, but the relative size of 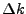 becomes smaller as
becomes smaller as
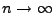 ,
so if we write,and so we find loose enough reason to approximate, for
,
so if we write,and so we find loose enough reason to approximate, for 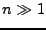 ,
,
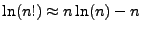 |
(1.3) |
root
2006-09-15