


Next: Result
Up: Detailed Derivation of the
Previous: The Summation Transform
The proper method of limiting this point to the real axis is to give the line of integration
a small semi-circle bump below the real axis to accommodate the point. One then takes the
radius of this semi-circle to zero and achieves the proper integral. It can be shown that the
proper form of this integration is given by
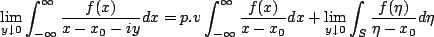 |
(6.1) |
The latter is taken over a semicircle which can be shrunk in the limit and thus equals
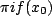 . Using
the postulate of the Dirac delta function, we can write,
. Using
the postulate of the Dirac delta function, we can write,
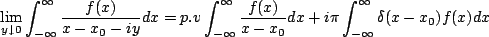 |
(6.2) |
This is typically approximated in theoretical physics as,
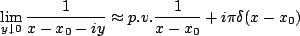 |
(6.3) |
We note that, with 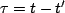 ,
,
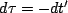 ,
,
![$\displaystyle -\int^t_0 \exp(i(\omega-\omega_j)\tau)d\tau = \left(\frac{i}{\omega-\omega_j}\right)[1-\exp(i(\omega-\omega_j)t)]$](img116.png) |
(6.4) |
The exponential term approximately averages out over the  integration, and we have the approximation,
integration, and we have the approximation,
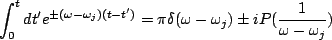 |
(6.5) |
Now looking at the table of calculations on the previous page, we see that many principal value part terms will cancel out,
specifically, the B and C terms (i.e. 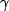 cancels
cancels
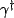 whenever all other terms are equal).
whenever all other terms are equal).
For the A D terms, we must do something fancy, that is, use that
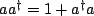 to convert all terms
to
to convert all terms
to
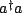 terms. This will create terms with
terms. This will create terms with  operators, but we notice the symmetry between these terms and that
they cancel. We also see the antisymmetry across each row for the A and D terms, but since
operators, but we notice the symmetry between these terms and that
they cancel. We also see the antisymmetry across each row for the A and D terms, but since
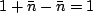 , we
are left with only one set of terms which retain their principal value part.
, we
are left with only one set of terms which retain their principal value part.
We could articulate these details, but we feel that it will profit the reader to examine this by the table presented
in this report.
The Dirac delta function will act as we would expect and drop out the 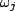 terms to
terms to  , and so we will
have our final terms.
, and so we will
have our final terms.



Next: Result
Up: Detailed Derivation of the
Previous: The Summation Transform
Timothy Jones
2006-10-11
![]() to convert all terms
to
to convert all terms
to
![]() terms. This will create terms with
terms. This will create terms with ![]() operators, but we notice the symmetry between these terms and that
they cancel. We also see the antisymmetry across each row for the A and D terms, but since
operators, but we notice the symmetry between these terms and that
they cancel. We also see the antisymmetry across each row for the A and D terms, but since
![]() , we
are left with only one set of terms which retain their principal value part.
, we
are left with only one set of terms which retain their principal value part.
![]() terms to
terms to ![]() , and so we will
have our final terms.
, and so we will
have our final terms.