Ordinary Differential Equations

Solving differential equations is central to doing Physics. In this section we will consider ordinary differential equations---ODEs, which occur when there is only one independent variable in the problem. The generic first-order differential equation is

where f is an arbitrary function and y may be a scalar or a vector quantity. In the vector case, and the equation

is equivalent to the n coupled scalar equations:

Well known second-order examples are the motion of a particle in a general force field:

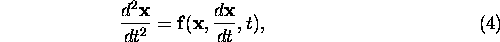
and the (one-dimensional) time-independent Schrödinger equation:

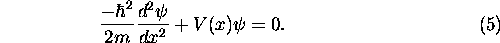
Later, we will turn our attention to the more complex partial differential equations---PDEs, in which two or more independent variables are involved. The prime example of such a system is the Wave Equation:

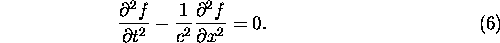
For now, however, let's start with something simple!

All ODEs can be reduced to an equivalent set of first-order equations, similar in form to equations (2) or (3) above. For example, in the second-order (one-dimensional) version of equation (4):

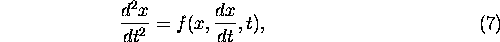
we can define the vector by

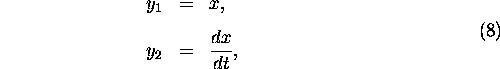
so that equation (7) becomes:

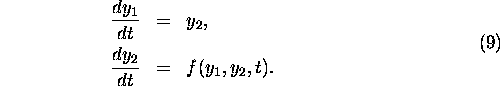
Such a transformation can always be carried out, so, without loss of generality, we need only consider equations like (2) from here on.

In general, an n-th order equation (i.e. in n dimensions, or involving derivatives up to order n, or some equivalent combination) requires n independent pieces of information--- boundary conditions---to define it fully. ODEs are classified according to the way in which the boundary conditions are specified. In initial-value problems, all boundary conditions are given at one particular value of the independent variable---typically time. These equations are generally the simplest to solve. We just set the initial conditions and integrate into the future, with no contraints on the evolution of the system. A good example is projectile motion, in which we specify x and v at time t = 0, then ask where the particle is at later times.

In boundary-value problems, the boundary conditions are specified at two or more values of the independent variable (now typically spatial). For example, in the Schrödinger equation, we may wish to specify the value of the wave function at two locations. These equations are typically much more tricky to solve, as they generally involve iteration to find a solution satisfying all the constraints. Notice that a boundary-value problem must be at least second-order (or two-dimensional).

As a matter of notation (and common usage), we will use t (time) as the independent variable and x (position) as the dependent variable in initial-value problems. For boundary-value problems, we will use x (a spatial quantity) as the independent variable.