

Gravitational Flexion (pronounced "flecks-shun" for the uninitiated, and yes, it is a real word) is a new technique for measuring 2nd order gravitational lensing signals in background galaxies and radio lobes.
Unlike shear, flexion directly probes variations of the potential field. Moreover, the information contained in flexion is orthogonal to what is found in the shear. Thus, we get the information "for free."
Some Recent Results
 |
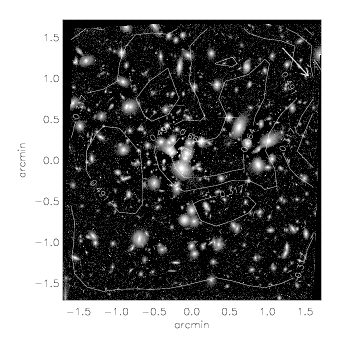 |
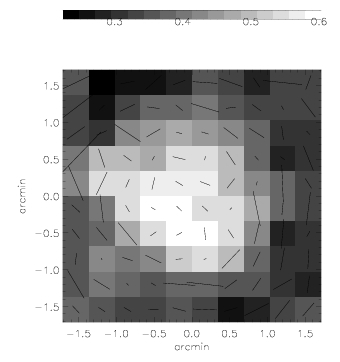
| Shear map of A1689. | Strong+Weak Reconstruction of A1689 (Using the Bradac et al. reconstruction method) |
 |
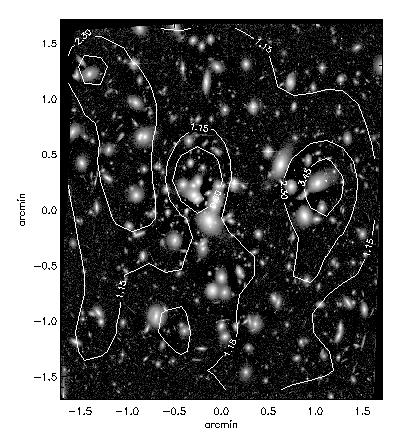 |
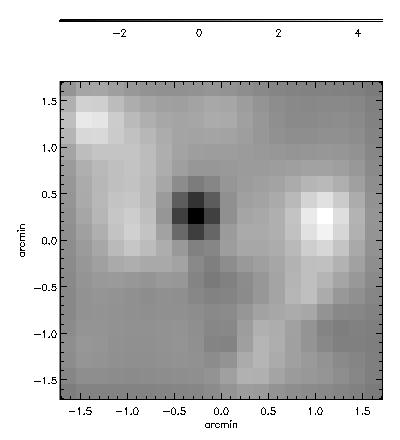
| Parametric density reconstruction using flexion. | Contour map of the same reconstruction. |
Flexion Papers
This is a paper I wrote with Priya Natarajan, while working for her at Yale. In it, we lay out the basic formalism for using 2nd order perturbation theory to study gravitational lensing. The math is a bit messy, I'm afraid.
This paper was written with David Bacon of the Royal Observatory, Edinburgh. In it, we use the shapelets formalism developed by Alexandre Refregier to flesh out the shapelets technique. We also show its viability by measuring the galaxy-galaxy flexion signal from the Deep Lens Survey.
This is a theoretical paper which explores many potential future avenues of flexion analysis: measurements in clusters, galaxy-galaxy flexion, cosmic flexion, and so on. Plus, Andy Taylor introduces a really nice complex space formalism that not only works for flexion, but for shear as well. You'll love it!
This paper does a good job showing that flexion is expressible as octopole moments (HOLICs). We have an implementation of the basic technique available in the flexion package above.
We introduce a KSB-type inversion technique for the HOLICs approach, and do an observational comparison between shapelets and HOLICs.
Richard Massey and the gang derive flexion and shear relations with a new set of polar basis functions.
Adrienne led this effort to combine non-parametric reconstructions using shear (shapelets), with multiple images (strong lensing), as well as parametric reconstructions using flexion in the rich cluster A1689.
This paper addresses analytic estimates of flexion in elliptical potentials.
Schneider and Er address the tricky question of reduced flexion as the true observable.
Okura et al. further refine the flexion analysis using HOLICs, including development of formalism to deal with anisotropic shear. They also produce a remarkable analysis of A1689. Using Flexion only, they identify to central density peaks which clearly correspond to peaks in galaxy counts. Remember, folks, this is on a scale of only 1 arcminute!

I know what you're thinking: "Looking at the flexion papers, there's no way that I can code all of that!" Well, you're in luck, I have some idl code (which, presumably, can be translated into C or fortran or whatever with a judicious use of search and replace), which calculates flexion:
Drexel folks
Dave Goldberg -- which is to say, me. I'll be happy to answer any and all of your shapelets questions.
Sanghamitra Deb -- Sanghamitra is a graduate student working on combining strong and weak lensing techniques in novel ways.
Jason Haaga -- Jason is an undergraduate co-op student who worked with us on the reconstruction of A1689.
Cambridge folks
Adrienne Leonard -- Adrienne did her master's thesis with me at Drexel, and is now at Cambridge doing her Ph.D. with Lindsay King. She led the effort to measure shear and flexion in A1689.
Edinburgh folks
David Bacon -- David is a PPARC Fellow at the Royal Observatory. He and I worked out the basic flexion formalism and made the first real measurements.
Barnaby Rowe -- Barney is a graduate student working with David on measuring flexion in the GEMS Survey.
Andy Taylor -- As mentioned above, Andy came up with a very nice way of expressing shear, first and second flexion using complex notation.
Caltech folks
Richard Massey -- Richard is the author of some very fine shapelets codes. He is also working on measuring flexion.
Related Work
John Irwin & Marina Shmakova have done related work measuring the Sextupole moments. What we term "Flexion" is referred to in their work as displacements (1st flexion) and cardioids (2nd flexion). They have a novel technique of correlating these terms with the shear as a means of detecting the signal, and have done so in the Hubble Ultra-Deep Field with co-author Jay Anderson.
Yuki Okura, Keiichi Umetsu, and Toshifumi Futamase have developed a
very intuitive approach to measuring flexion -- direct measurement of
the octopole moments. They have done the full inversion of these
moments (which we did not do in Goldberg & Natarajan). They refer to
their method as Higher Order Lensing Image's Characteristics or HOLICs, and it
may hold the key to fast estimate of flexion in large fields.
Indeed, they have applied there technique to A1689 (see above), and
have done a remarkable job on direct detection of substructure within
the cluster using flexion alone.
Edward Baltz, Phil Marshall, and Msaamune Oguri explored analytic models of flexion for elliptical potentials.
Peter Schneider and his student, Xinzhong Er have recently addressed a very thorny issue -- the reduced flexion. As with any lensing system, the reconstructed flexion field actually corresponds to a single solution among an entire degenerate class of solutions. This is the well-known "mass-sheet degeneracy." Schneider and Er relate the observed 3rd moments of images to the reduced flexion and show how these can be used to reconstruct a density field.
This page is written, maintained, and edited by Dave Goldberg. Last edited 9/18/07.