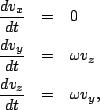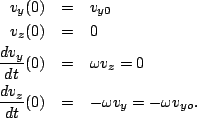

Next: About this document ...
Up: Solutions
Previous: Solutions
This is a very good, but rather difficult problem. We want to solve for the velocity as a function of time, so we're looking to solve the equation of motion. But, before we do it analytically, lets think about the solution. We know the magnetic field does not act on a component of velocity parallel to it (remember the cross product?). So, the x-component here will remain unchanged. Now, the y-component is now perpendicular to B. But, the magnetic field can only change its direction.
Now the right hand rule says that force is upward. So the y-component begins to rotate upward. But, as it rotates, the force changes so as always to be perpendicular to the velocity direction. In other words, this is a problem of centripetal acceleration! The direction of the perpendicular component will go around in a circle, but with always the same magnitude.
Now, put the two together. The parallel component of velocity remains unaltered, while the perpendicular component goes around in a circle - the path should be that of a helix, or spring. In fact, if we continue our analysis along these lines we can get the precise mathematical form of the answer. Try it and see if you get what is derived below through some labor.
Now, lets look at this analytically. We want to solve the equations of motion, so we have Newton's equation
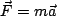 , with the magnetic force on the left-hand-side. Thus we have
, with the magnetic force on the left-hand-side. Thus we have
where the complication arises because  is on both sides - we have a differential equation.
is on both sides - we have a differential equation.
But, we can expand out  in terms of it's components and take the cross product with
in terms of it's components and take the cross product with 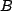 as follows:
as follows:
which follows using the rules above (note that the 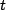 's have been dropped for ease of notation). Now using this expression, Newton's equation becomes
's have been dropped for ease of notation). Now using this expression, Newton's equation becomes
This is a vector equation, which stands for 3 separate equations when written out in components:
where we have set
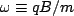 for convenience. The first equation is easy - no acceleration in x. The x-velocity never changes so
for convenience. The first equation is easy - no acceleration in x. The x-velocity never changes so 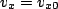 for all time.
for all time.
The second two equations, however, are rather nasty - coupled differential equations. They are coupled because the change in one depends on the current value of the other. However, it is actually not too difficult to work this out. Treat it like any other system of equations with two unknowns - try to eliminate variables and then solve for the unknowns. For instance, the second equation gives
We can then substitute this expression into the third equation to obtain
If we do the same procedure with 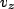 we get the same thing but with
we get the same thing but with 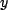 replaced by
replaced by 
Voila! The equations have been decoupled. Now, we need to solve these two (identicle) equations - we need functions that, after differentiated twice, give the the same thing back but with a minus sign. A little though or intuition will yield
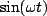 and
and
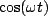 (you can check these by differentiation).
(you can check these by differentiation).
Now, which do we use? Or do we use both? Here is where the initial conditions come in. Our initial conditions are
Thus, the equation for 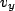 should start at its maximum value (first and third equations) and should just be given by
should start at its maximum value (first and third equations) and should just be given by 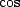 . Likewise, for
. Likewise, for 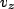 we start at zero, but have maximal, negative, derivative, which means
we start at zero, but have maximal, negative, derivative, which means 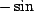 . Thus
. Thus
You can verify by substitution that these satisfy the coupled differential equations and our initial conditions exactly. Our full solution is therefore
which describes a helical path as advertised (and
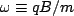 is the cyclotron frequency). Finally, given
is the cyclotron frequency). Finally, given 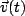 above, can you find
above, can you find 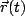 ?
?


Next: About this document ...
Up: Solutions
Previous: Solutions
Daniel Cross
2006-09-18
![]() , with the magnetic force on the left-hand-side. Thus we have
, with the magnetic force on the left-hand-side. Thus we have
![]() in terms of it's components and take the cross product with
in terms of it's components and take the cross product with ![]() as follows:
as follows: